Unizor - Physics4Teens - Mechanics - Work - Problems

Notes to a video lecture on http://www.unizor.com



Problems on Mechanical Work



Problem A



An object of mass m is pushed up a plane inclined to horizon at angle φ with constant acceleration a to a height h against a friction with coefficient of kinetic friction μ.

(a) What is the amount of work necessary to achieve this goal?



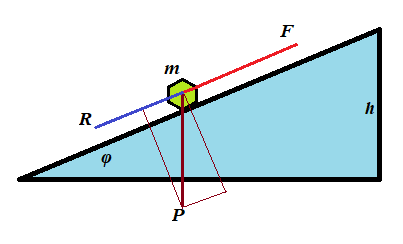
(b) Consider the following real conditions of this experiment:

m = 10kg(kilograms)

g = 9.8m/sec²(meters per sec²)

h = 0.5m(meters)

φ = 30°(degrees)

μ = 0.2

a = 0.1m/sec²(meters per sec²)

The work W=F·S is measured in N·m=kg·m²/sec² units, called joule and abbreviated as J.

Calculate the work W performed in this experiments in joules.



Solution

Let F be the force that pushes the object up the slope, P=m·g is the object's weight, R is the force of resistance from the friction, S is the distance this object moves to reach the height h.

(a) F−P·sin(φ)−R = m·a

R = P·cos(φ)·μ

W = F·S

S = h/sin(φ)

F = P·sin(φ) + R + m·a =

= m·[g·sin(φ) + g·cos(φ)·μ + a]

W = F·h/sin(φ) =

=m·h[g+g·cot(φ)·μ+a/sin(φ)]

(b)
W = 67J(joules)





Problem B



An object of mass m is pushed by a constant force F down a slope of a plane inclined to horizon at angle φ. Initially, it's at rest, the final speed is V. There is a friction with coefficient of kinetic friction μ.

(a) What is the time t from the beginning to the end of the object's motion?

(b) What is the distance S this object moved until reaching the final speed V?

(c) What is the amount of work W performed by this force?

(d) Consider the following real conditions of this experiment:

F = 20N(newtons)

m = 10kg(kilograms)

g = 9.8m/sec²(meters per sec²)

V = 0.5m/sec(meters per sec)

φ = 5°(degrees)

μ = 0.7

Calculate the work W performed in this experiments in joules, distance S and time t of motion.



Solution

P=m·g is the object's weight,

R = P·cos(φ)·μ is the force of resistance from the friction,

S is the distance this object moves to reach the speed V,

a is the acceleration of this object.

Then from the Newton's Second Law

F+P·sin(φ)−R = m·a

(we added P·sin(φ) because an object moves down a slope)

Now we can find an acceleration of our object:

F+m·g·sin(φ)−m·g·cos(φ)·μ =

= m·a

a = F/m + g·sin(φ) − g·cos(φ)·μ

Knowing acceleration a and the correspondence between acceleration, final speed and time V=a·t, we can determine time:

(a) t = V/a

Now we can find the distance

(b) S = a·t²/2 = V·t/2

The work performed by the force F equals to

(c) W = F·S

(d) a = 0.066(m/sec²)

t = 7.576(sec)

S = 1.894(m)

W = 37.879(joules))





Problem C



An object of mass m is dropped down from a certain height above a surface of some planet. At the moment it hits the ground its speed is V.

What is the work W performed by the force of gravity?



Solution

Let the acceleration of free falling on this planet is a, the time of falling t and the height S.

Then

F = m·a

V = a·t

t = V/a

S = a·t²/2 = V²/(2·a)

W = F·S = m·V²/2

Notice, the work depends only on mass and final speed - the results of
action, not on the height, nor acceleration of free falling, nor on
time.