Unizor - Physics4Teens - Energy - Energy of Gravitational Field - Gravit...

Notes to a video lecture on http://www.unizor.com

Gravity Integration 1

Determine the potential of the gravitational field of an infinitely thin solid rod at any point outside of it.

Let's establish a system of coordinates with a rod and a point mass lying in the XY-plane with the rod on the X-axis with one end at point A(a,0) and another at point B(b,0).
Assume that the rod's length is L=b−a and the mass is M, so the density of mass per unit of length is ρ=M/L.
Assume further that the coordinates of a point P, where we want to calculate the gravitational potential, are (p,q).

If, instead of a rod, we had a point mass M concentrated in the midpoint of a rod at point ((a+b)/2,0), its gravitational potential at a point (p,q) would be
V₀=G·M/r
where r is the distance between the midpoint of a rod and a point of measurement of gravitational potential P:
r = {[(p−(a+b)/2]² + q²}^1/2

Since the mass in our case is distributed along the rod, the gravitational potential will be different.

As we know, gravitational potential is additive, that is the potential of a combined gravitational field produced by two or more sources of gravitation at some point equals to sum of their individual gravitational potentials at this point.
Therefore, to calculate a gravitational potential of a rod, we can divide it into infinite number of infinitesimal pieces, calculate the gravitational potential of each piece at the point of interest P and integrate all these potentials.

Consider a picture below (we recommend to save it locally to see in the bigger format).

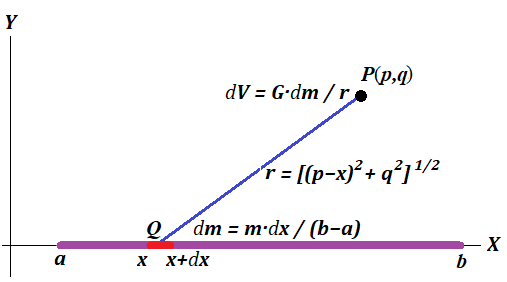
As a variable, we will use an X-coordinate of a point on a rod Q and calculate the gravitational potential at point of interest P(p,q) from an infinitesimal segment of a rod of the length dx around point Q(x,0).
Knowing that, we will integrate the result by x on a segment [a;b] to get the gravitational potential of the rod.

The infinitesimal segment of a rod dx, positioned around a point Q(x,0), has an infinitesimal mass dm that can be calculated based on the total mass of a rod M and its length L=b−a as
dm = M·dx /L

The gravitational potential of this segment depends on its mass dm and its distance r(x) to a point of interest P(p,q).
dV = G·dm /r(x)
Obviously,
r(x) = [(p−x)²+q²]^1/2
Combining all this, the full gravitational potential of a rod [a;b] of mass M at point P(p,q) will then be
V(p,q) = ∫_a^bG·dm /r(x) = ∫_a^bG·M·dx/{L·[(p−x)²+q²]^1/2}

We can use the known indefinite integral
∫dt /√(t²+c²) = ln|t+√(t²+c²)|

Let's substitute in the integral for gravitational potential t=x−p.
Then
V(p,q) = ∫G·M·dt /L·[t²+q²]^1/2
where integration is from t=a−p to t=b−p.
V(p,q) = (G·M/L)·[ln|b−p+√(b−p)²+q²| − ln|a−p+√(a−p)²+q²|]
where L = b−a

Since the difference of logarithms is a logarithm of the result of division,
V(p,q) = G·M·ln(R) /L
where
L = b−a and
R = |b−p+√(b−p)²+q²| / |a−p+√(a−p)²+q²|