Notes to a video lecture on http://www.unizor.com
Problems on Gravity
Problem 1
Gravitational potential of a spherical gravitational field around a point-mass M at a distance r from it is defined as the work performed by gravity to bring a probe object of a unit mass from infinity to this point and is expressed as
Vr = −G·M /r
Why is this formula independent of trajectory of a probe object or its exact final position relative to the point-mass M, but only on a distance itself from the source of gravity?
Solution
Any movement can be represented as infinitely many infinitesimal displacements, combined together into a trajectory.
In our three-dimensional world the force and an infinitesimal displacement of a probe object are vectors, so the infinitesimal work dW performed by the force of gravity F during the movement of a probe object, described by the infinitesimal displacement dS, is a scalar product of these two vectors:
dW = F·dS
Note that the vector of gravitational force F is always directed towards the source of gravity.
Since a displacement vector dS can be represented as a sum of radial (towards the source of gravity) dSr and tangential (perpendicular to radius) dSt components, the above expression for a differential of work can be written as
dW = F·(dSr + dSt) =
= F·dSr + F·dSt
The second component in the above expression is a scalar product of two perpendicular vectors and is equal to zero. That's why we can completely ignore tangential movements, when calculating the work done by a central gravitational field, as not contributing to the amount of work. The total amount of work will be the same as if our probe object moved along a straight line towards the source of gravity and stopped at a distance r from it.
Problem 2
Given two point-masses of mass M each, fixed at a distance 2R from each other.
Prove that the gravitational potential of a gravitational field produced by both of them at each point on a perpendicular bisector between them equals to a sum of individual gravitational potentials of these point-masses at this point, as if they were the only source of gravitation. In other words, prove that gravitational potential is additive in this case.
Solution
Let's draw a diagram of this problem (you can download it to display in a bigger format).
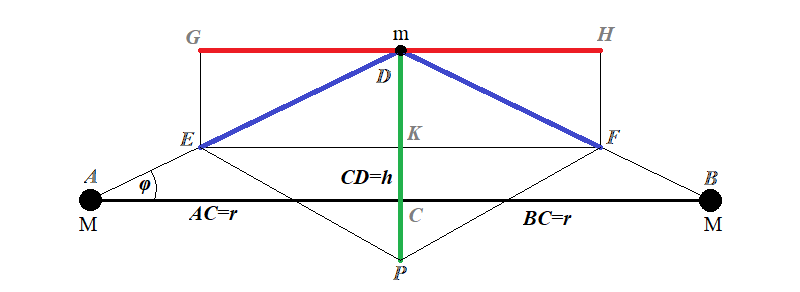
Our two point-masses are at points A and B, the probe object is at point D on a perpendicular bisector of a segment AB going through point C.
The force of gravity towards point A is a segment DE, the force of gravity towards point B is a segment DF.
We will calculate the potential of a combined gravitational field of two point-masses at point D, where the probe object is located.
Let's assume that the segment CD equals to h.
The magnitude of each gravitational force equals to
F = G·M·m /(h2+r2)
Represent each of these forces as a sum of two vectors, one (green on a drawing) going vertically along the bisector CD, another (red) going horizontally parallel to AB.
Vertical components of these two forces will add to each other, as equal in magnitude and similarly directed downwards on a drawing, while horizontal ones will cancel each other, as equal in magnitude and opposite in direction to each other. So, the combined force acting on a probe object is a sum of vertical components of gravitational forces with a magnitude
Ftot = 2·G·M·m·sin(φ)/(h2+r2)
Since sin(φ) = CD/AD,
sin(φ) = h /[(h2+r2)1/2]
Ftot = 2·G·M·m·h /(h2+r2)3/2
If the gravitational field pulls a probe object along the perpendicular bisector of a segment AB from infinity to a distance h from the segment, the magnitude of a combined force of gravity, as a function of a distance from the segment x is changing, according to a similar formula:
Ftot(x) = 2·G·M·m·x /(x2+r2)3/2
To calculate work performed by a gravitational field pulling a probe object from infinity to height h above the segment AB, we have to integrate
Wtot = ∫[∞;h]Ftot(x)·dx
It's supposed to be negative, since the direction of a force is opposite to a positive direction of the coordinate axis, we will take it into account later.
Wtot = ∫2GMm·x·dx /(x2+r2)3/2
(within the same limits of integration [∞;h])
This integral can be easily calculated by substituting
y=x2+r2,
2·x·dx = dy,
infinite limit of integration remaining infinite and the x=h limit transforming into y=h2+r2. Now the work expression is
Wtot = ∫G·M·m·y−3/2·dy
with limits from y=∞ to y=h2+r2.
The indefinite integral (anti-derivative) of y−3/2 is −2·y−1/2.
Therefore, the value of integral and the work are
Wtot = −2·G·M·m·(h2+r2)−1/2
For a unit mass m=1 this work is a gravitational potential of a combined gravitational field produced by two point-masses on a distance h from a midpoint between them along a perpendicular bisector
Vtot = −2·G·M·(h2+r2)−1/2
At the same time, the gravitational potential of a field produced by each one of the point-masses, considered separately, equals to
Vsingle = −G·M·(h2+r2)−1/2
As we see, the gravitational potential of two point-masses equals to a sum of gravitational potential of each of them, considered separately.
IMPORTANT NOTE
With more cumbersome calculations this principle can be proven for any two (not necessarily equal) point-masses at any point in space (not necessarily along the perpendicular bisector). This principle means that gravitational potential is additive, that is the gravitational potential of any set of objects at any point in space equals to sum of their individual gravitational potentials.
Problem 3
Express mass M of a spherical planet in terms of its radius R and a free fall acceleration g on its surface.
Solution
Let m be a mass of a probe object lying on a planet's surface.
According to the Newton's 2nd Law, its weight is
P = m·g
According to the Universal Law of Gravitation, the force of gravitation between a planet and a probe object is
Fgravity = G·M·m /R2
Since the force of gravitation is the weight Fgravity = P,
m·g = G·M·m /R2
from which
M = g·R2 /G
Problem 4
Express gravitational potential VR of a spherical planet on its surface in terms of its radius R and a free fall acceleration g on its surface.
Solution
From the definition of a gravitational potential on a distance R from a source of gravity
VR = −G·M /R
Using the expression of the planet's mass in terms of its radius R and a free fall acceleration g on its surface (see above),
M = g·R2 /G
Substituting this mass into a formula for potential,
VR = −G·g·R2 /(G·R) = −g·R


No comments:
Post a Comment