Notes to a video lecture on http://www.unizor.com
Electric Field Intensity
Electric field intensity is the force (based on the Coulomb's Law) of an electric field of some electrically charged object A, exhorted on a probe point-object B, charged with one coulomb of positive electricity (+1C), positioned at some point in the electric field around a main object A.
In other words, it's the force experienced by a probe point-object, charged with +1C of electricity, positioned at some point in space around a main electrically charged object A.
This is a measure of the intensity of the electric field of some charged object at a specific point in space. So, it's a function of two parameters: the electric charge in the main object A and a position in space relatively to this object.
In many cases the word "intensity" is replaced with a word "strength" or just dropped from the conversation. So, terms electric field intensity, electric field strength or in some cases simply electric field are synonymous.
First of all, electric field intensity is a force and, therefore, a vector. Since electrically charged objects attract or repel each other, depending on the type of their charges (positive with deficiency of electrons or negative with excess of electrons), this force is directed along the line connecting a main object, whose electric field intensity we measure, and a probe point-object, charged with +1C of electricity, positioned somewhere in space around the main object.
The magnitude of the vector of electric field intensity can be calculated based on the Coulomb's Law.
The general form of the Coulomb's Law, when two electrically charged point objects, A and B, are involved, is
E = k·qA·qB / R²
where
E is the magnitude of the force of attraction (in case of opposite charges) or repelling (in case of the same type of charge, positive or negative) in N - newtons
qA is electric charge of point-object A in C - coulombs
qB is electric charge of point-object B in C - coulombs
R is the distance between charged objects in m - meters
k is a coefficient of proportionality, equals to 9.0·109 in N·m²/C²
Since the electric charge of a probe point-object B, that we use to measure the intensity of an electric field of some charged point-object A, is qB=+1C, the magnitude of the electric field intensity of point-object A with electric charge qA at a distance R from it is
E = k·qA / R²
The direction of the vector of this force of electric field intensity is along the line connecting the main and the probe point-objects towards the main object, if its charge is negative and attracting a positively charged probe object, or away from the main object, if its charge is positive and repelling a positively charged probe object.
If two or more main point-objects charged with electricity are positioned in some configuration, a probe point-object will experience some force from each of them. All these forces will be combined, according to the rules of vector addition, and the resulting force is the intensity of the combined electric field of all main point-objects.
Example 1
Consider a pair of point-objects at points A and B, charged with positive charge +q each, at distance 2d from each other. What would be an intensity E(x) of their combined electric field at a point P on a perpendicular bisector of a segment AB at distance x from a midpoint M of this segment?
Magnitude of the intensity of electric field from each object is
EA = EB = k·q/(d²+x²)
One of them is directed from A to P, another - from B to P. They are at angle to each other, so we need the rule of parallelogram to find a resulting force. Let ∠APM be φ.
tan(φ) = d/x
Representing each field intensity vector as the sum of two vectors - one along the line MP and another along the line AB, and taking into consideration only the components along MP (the other two nullify each other), we can calculate the resulting intensity
E = EA·cos(φ) + EB·cos(φ) =
= 2k·q·cos(φ) / (d²+x²) =
= 2k·q·x / [(d²+x²)3/2]
Example 2
Consider an infinitely thin rod of a length 2d charged with electricity such that the density of electrical charge (amount of charge per unit of length) equals to λ.
Our task is to determine the electrical field intensity at any point outside this rod.
Let's establish the frame of reference with the origin of coordinates at the midpoint of our rod and the X-axis along a rod. So, the rod is positioned on the X-axis from x=−d to x=+d.
From the consideration of symmetry it is obvious that the two main parameters of the position in space are important: how far a point is from the X-axis and how far the projection of the point on the X-axis is from the center of the rod. This allows us to establish XY-plane as going through the rod and a point in space where the electric field intensity is supposed to be determined and ignore the Z-axis, so the position of the rod and a point, where intensity is to be established, can be represented on XY-plane as below.
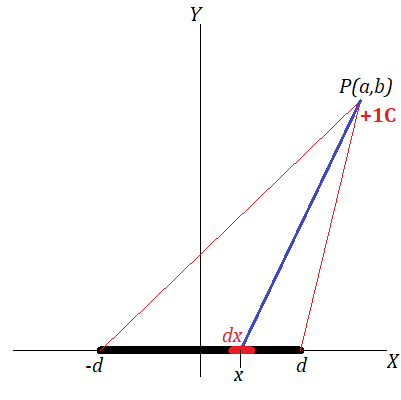
Point P(a,b) is the one, where the field intensity is to be established. Y-coordinate y=b represents the distance from point P to the rod along a perpendicular to the rod and X-coordinate represents the distance from the projection of point P on the X-axis to the midpoint of the rod.
The probe charge of +1C is at point P(a,b) and the field intensity at this point is the sum of all forces exhorted by the pieces of rod onto this probe charge.
Consider infinitesimal piece of the rod of the length dx positioned at X-coordinate x. The plan is to determine the force it exhort onto the probe charge of +1C at point P(a,b) and integrate the result from x=−d to x=d.
The electric charge of the piece of the rod of the length dx is λ·dx, where λ is the given density of electric charge in the rod.
The square of the distance r from this piece of the rod to point P(a,b) is
r² = (a−x)² + b²
Now we can apply the Coulomb's Law to determine the infinitesimal electric force dF between this piece of the rod of the length dx and a probe charge of +1C at point P(a,b)
dE = k·λ·dx / [(a−x)²+b²]
The above is the magnitude of the electrical force. Its direction is along the line connecting a piece of the rod with point P(a,b).
We cannot integrate this expression directly since the forces from different pieces of the rod have different direction. We have to represent this force as a sum of two forces - horizontal force Fx along the X-axis and vertical force Fy along the Y-axis. Then we can separately integrate each component to get two components of the final force.
Simple math gives us the following expressions for component of the force F
dEx = dE·(a−x) / r =
= k·λ·dx·(a−x) / [(a−x)²+b²]3/2
dEy = dE·b / r =
= k·λ·dx·b / [(a−x)²+b²]3/2
Now you see how important is Mathematics to succeed in Physics!
Let's integrate each force, horizontal and vertical, on x∈[−d,d] interval.
First, let's find indefinite integral for Ex
∫k·λ·dx·(a−x)/[(a−x)²+b²]3/2 =
...substitute y=(a−x)²+b²
= −0.5·k·λ·∫y−3/2dy =
= k·λ·y−1/2
Definite integral for y should be taken in limits from (a+d)²+b² to (a−d)²+b², which results in the following expression for Ex: Ex = k·λ·{[(a−d)²+b²]−1/2−[(a+d)²+b²]−1/2}
Incidentally,
rright = [(a−d)²+b²]1/2
is the distance from point P(a,b) to the right end of the rod and
rleft = [(a+d)²+b²]1/2
is the distance to the left end.
So, the formula for horizontal component of the resulting field force is
Ex = k·λ·[1/rright − 1/rleft]
Interestingly, as the length of the rod increases to infinity, the horizontal component of the field strength diminishes to zero, as both 1/rright and 1/rleft diminish to zero. The obvious reason is that with an infinitely long rod the horizontal forces directed to the left are balanced by horizontal forces directed to the right.
Now let's address the vertical component of the electric field intensity Ey.
First, let's calculate the indefinite integral
∫k·λ·dx·b / [(a−x)²+b²]3/2 =
...substitute (a−x)/b=tan(y)
...tan(y)=(a−x)/b
...(a−x)²+b² = b²·[tan²(y)+1] =
...= b²/cos²(y)
...[(a−x)²+b²]−3/2 = b−3·cos3(y)
...dx=−b/cos²(y)·dy
= −(k·λ/b)·∫cos(y)·dy =
= (k·λ/b)·sin(y) + C
As far as limits of integration, if x∈[−d,d] then y∈[y1,y2], where
y1 = arctan((a+d)/b) and
y2 = arctan((a−d)/b)
To find the definite integral in the limits above, we will use a trigonometric identity
sin(arctan(z)) = z / √(1+z²)
Now we can express the vertical component of the field intensity as
Ey = (k·λ/b)·[sin(y2)−sin(y1)]
where y1 and y2 are defined above.
Ey = (k·λ/b)·{(a−d)·[(a−d)²+b²]−1/2 − (a+d)·[(a+d)²+b²]−1/2}


No comments:
Post a Comment