Notes to a video lecture on http://www.unizor.com
Problems 3
Problem A
An infinitesimally thin sphere α of radius R is electrically charged with uniform density of electric charge σ (coulombs per square meter).
A point P is inside this sphere at a distance h (meters) from its center, so h is less than R.
What is the intensity of the electric field produced by this sphere at point P?
Solution
The magnitude of the field intensity at point P produced by any infinitesimal piece of sphere α is inversely proportional to a square of its distance to point P and directly proportional to its charge, and the charge, in turn, is proportional to its area with density σ being a coefficient of proportionality.
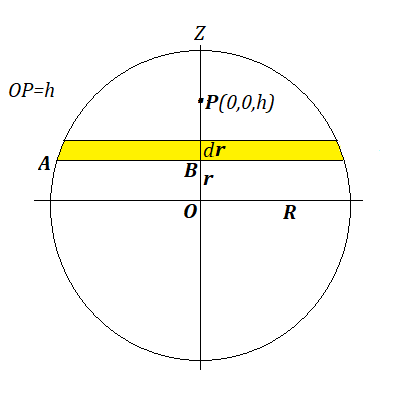
Let's define a system of Cartesian coordinates in our three-dimensional space with the origin at the center O of the center of the charged sphere α with Z-axis along segment OP.
Then the coordinates of point P, where we have to calculate the vector of electric field intensity, are (0,0,h).
From the considerations of symmetry, the vector of intensity of the field, produced by an entire electrically charged sphere α, at point P inside it should be directed along a line OP from point P to a center of a sphere, that is along Z-axis. Indeed, for any infinitesimal area of sphere α near point (x,y,z) there is an area symmetrical to it relatively to Z-axis near point (−x,−y,z), which produces the intensity vector of the same magnitude, the same vertical (parallel to OP) component of it and opposite horizontal component. So, all horizontal components will cancel each other, while vertical ones can be summarized by magnitude.
Therefore, we should take into account only projections of all individual intensity vectors from all areas of a sphere onto Z-axis, as all other components will cancel each other.
The approach we will choose is to take an infinitesimal area on a sphere in a form of a spherical ring of infinitesimal width, produced by cutting a sphere by two planes parallel to XY-plane at Z-coordinates z=r and z=r+dr and calculate the vertical component of the intensity vector produced by it. Then we will integrate the result from r=−R to r=R.
This choice is based on a simple fact that for every small piece of this spherical ring its distance to point P is the same, as well as an angle between its vector of intensity and Z-axis is the same, hence the vertical component of the field intensity vector produced by it will be the same as for any other such piece of this spherical ring, if it has the same area, while the horizontal component of the intensity vector will be canceled by a symmetrical piece of this spherical ring lying diametrically across it.
Since any infinitesimal part of this ring has exactly the same vertical component of the intensity vector as any other part having the same area, to get the total vertical component of intensity for an entire ring, we can use its total charge that depends on its total area and charge density σ.
The area of a spherical ring equals to a difference between areas of two spherical caps.
The area of a spherical cap equals to 2π·R·H, where H is the height of a cap.
The spherical cap formed by a plane cutting a sphere at z=r has height R−r. The spherical cap formed by a plane cutting a sphere at z=r+dr has height R−r−dr.
Therefore, the area of a spherical ring between these two cutting planes is
area(r,dr) =
= 2π·R·[(R−r)−(R−r−dr)] =
= 2π·R·dr
The charge concentrated in this spherical ring is
dQ(r) = 2π·σ·R·dr
To find the magnitude of the intensity vector produced by this ring we need to know its charge (calculated above) and the distance to a point, where the intensity is supposed to be calculated. This distance can be calculated using the Pythagorean Theorem:
L² = (R² − r²) + (h−r)² =
= R² + h² −2h·r
The magnitude of the intensity vector produced by this spherical ring is, therefore,
dE(h,r) = k·dQ(r)/L² =
= 2π·k·σ·R·dr / L² =
= 2π·k·σ·R·dr / (R²+h²−2h·r)
We are interested only in vertical component of this vector, which is equal to
dEz(h,r)= dE(h,r)·sin(∠PAB) =
= dE(h,r)·(h−r)/L =
= 2π·k·σ·R·dr·(h−r) / L³ =
= 2π·k·σ·R·dr·(h−r) / (R²+h²−2h·r)3/2
Integrating this by r from −R to R can be done as follows.
First of all, let's substitute
x = R²+h²−2h·r
Then
r = (R²+h²−x)/2h
dr = −dx/2h
The limits of integration for x are from R²+h²+2h·R=(R+h)² to R²+h²−2h·R=(R−h)².
Now the expression to integrate looks like
dEz(h,x) = C·(h²−R²+x)·x−3/2·dx
where constant C equals to
C = −π·k·σ·R/(2h²)
Let's integrate the above expression in the limits specified.
First, find the indefinite integral.
∫C·(h²−R²+x)·x−3/2·dx =
= −2C·(h²−R²)·x−1/2 + 2C·x1/2 =
= 2C·[(R²−h²)·x−1/2 + x1/2]
This expression for indefinite integral should be used to calculate the definite integral in limits for x from (R+h)² to (R−h)².
Assuming that point P is inside a sphere, that is h is less than radius R,
((R+h)²)1/2 = R+h
((R−h)²)1/2 = R−h
Therefore, substituting the upper limit into an expression for an indefinite integral, we get
2C·[(R²−h²)/(R−h) + (R−h)] = 4C·R
Substituting the lower limit, we get
2C·[(R²−h²)/(R+h) + (R+h)] = 4C·R
The difference between these two expressions is zero, which means that the intensity of the electric field inside a uniformly charged sphere is zero.
Problem B
An infinitesimally thin sphere α of radius R is electrically charged with uniform density of electric charge σ (coulombs per square meter).
A point P is outside this sphere at a distance h (meters) from its center, so h is greater than R.
What is the intensity of the electric field produced by this sphere at point P?
Solution
Start as in the previous problem up to indefinite integral
2C·[(R²−h²)·x−1/2 + x1/2]
Assuming that point P is outside a sphere, that is h is greater than radius R,
((R+h)²)1/2 = R+h
((R−h)²)1/2 = h−R
Therefore, substituting the upper limit into an expression for an indefinite integral, we get
2C·[(R²−h²)/(h−R) + (h−R)] = −4C·R
Substituting the lower limit, we get
2C·[(R²−h²)/(R+h) + (R+h)] = 4C·R
The difference between them is the intensity of the electric field produced by a sphere at a point outside it:
E(h) = −8C·R =
= 8π·k·σ·R²/(2h²) =
= 4π·k·σ·R²/h²
Notice that
area(Sphere) = 4π·R²
Therefore, Q = 4π·σ·R²
where σ is the density of electric charge on a sphere, represents a total charge of a sphere.
Hence,
4π·k·σ·R²/h² = k·Q/h²
and the field intensity of a sphere at a point outside it equals to intensity of a point-object with the same electric charge and located at the center of a sphere.


No comments:
Post a Comment