Forced Oscillation 2 -
Resonance
This lecture continues analysis of forced oscillations for a specific case, when the angular frequency of external periodic force equals to an inherent natural frequency of an object on a spring without any external forces.
Let us remind the introductory material from the previous lecture.
Oscillation is forced, when some periodic force is applied to an object that can potentially oscillate.
A subject of our analysis will be an object on a spring with no other forces acting on it except one external force that we assume is periodical.
As we know, in the absence of external force the differential equation describing the displacement x(t) from a neutral position of an object of mass m on a spring of elasticity k follows from the Hooke's Law and the Newton's Second Law
m·x"(t) = −k·x(t)
or
m·x"(t) + k·x(t) = 0
with a general solution
x(t) = A·cos(ω0·t) + B·sin(ω0·t)
where
A and B are any constants;
ω0 = √k/m is an inherent natural angular frequency of oscillation of this particular object on this particular spring.
The equation above is homogeneous because, together with any its solution x(t), the function C·x(t) will be a solution as well.
Consider a model of forced oscillation of an object on a spring with a periodic external force F(t)=F0·cos(ω·t).
Previous lecture was dedicated to a case of angular frequency of an external force ω to be different from the inherent natural frequency of an object on a spring ω0.
In this lecture we consider a case of angular frequency ω of the periodic external function F(t)=F0·cos(ω·t) to be equal to the inherent natural angular frequency ω0=√k/m of oscillations without external forces:
ω = ω0 = √k/m
So, from now on we will use only symbol ω for both inherent natural angular frequency of a spring with an object without external forces and for an angular frequency of an external force.
If external force F(t), described above, is present, the differential equation that describes the oscillation of an object looks like
m·x"(t) = −k·x(t) + F(t)
or, assuming the external force is a periodic function F(t)=F0·cos(ω·t),
m·x"(t)+ k·x(t) = F0·cos(ω·t)
where ω=√k/m
The function on the right of this equation makes this equation non-homogeneous.
Our task is to analyze the movement of an object on a spring in the presence of a periodic external function, as described by the above differential equations and some initial conditions.
Notice that if some non-homogeneous linear differential equation has two partial solutions x1(t) and x2(t), their difference is a partial solution to a corresponding homogeneous linear differential equation.
Indeed, if
m·x1"(t)+ k·x1(t) = F0·cos(ω·t)
and
m·x2"(t)+ k·x2(t) = F0·cos(ω·t)
then for x3(t)=x1(t)−x2(t)
m·x3"(t)+ k·x3(t) = 0
From the above observation follows that, in order to find a general solution to a non-homogeneous linear differential equation, it is sufficient to find its one partial solution and add to it a general solution of a corresponding homogeneous equation.
In our case we already know the general solution to a corresponding homogeneous equation
m·x"(t)+ k·x(t) = 0
So, all we need is to find a single partial solution to
m·x"(t)+ k·x(t) = F0·cos(ω·t)
where ω=√k/m
and add to it the general solution to the above homogeneous equation.
In the previous lecture, where we considered an angular frequency of external force ω to be different from the inherent natural frequency of oscillation of an object on a spring ω0, we were looking for a partial solution in a form xp(t)=C·cos(ω·t) and found such a coefficient C that the equation is satisfied:
C = F0 / [m·(ω0²−ω²)]
But, if ω=ω0=√k/m, we cannot use this method (since denominator becomes zero) and have to invent something new.
The usual recommendation in a case like this is to still use trigonometric functions, but with some simple function as a multiplier.
Let's try the following function:
xp(t) = Q·t·sin(ω·t)
Let's find second derivative of xp(t), substitute xp(t) and x"p(t) into our differential equation and find suitable values for a constant Q. That would deliver a partial solution to our non-homogeneous differential equation.
x'p(t) =
= Q·sin(ω·t) + Q·t·ω·cos(ω·t)
x"p(t) = Q·ω·cos(ω·t)+
+Q·ω·cos(ω·t)−Q·t·ω²·sin(ω·t)
Our original equation
m·x"(t)+ k·x(t) = F0·cos(ω·t)
can be written as
x"(t) + (k/m)·x(t) =
= (F0/m)·cos(ω·t)
or
x"(t)+ω²·x(t) = (F0/m)·cos(ω·t)
Substitute the partial solution expression into the left part of the differential equation above:
Q·ω·cos(ω·t)+Q·ω·cos(ω·t)−
−Q·t·ω²·sin(ω·t)+Q·t·ω²·sin(ω·t)
Canceling positive and negative terms that are equal by absolute value, got the following equation with the proposed solution
2Q·ω·cos(ω·t) =
= (F0/m)·cos(ω·t)
from which
Q = F0/(2m·ω)
The partial solution to our non-homogeneous differential equation is
xp(t) = F0·t·sin(ω·t)/(2m·ω)
Now we can express the general solution to a differential equation that describes the forced oscillation by a periodic external function as
x(t) = F0·t·sin(ω·t)/(2m·ω) +
+ A·cos(ω·t) + B·sin(ω·t)
where
A and B are any constants determined by initial conditions x(0) and x'(0);
ω = √k/m is an inherent natural angular frequency of oscillation of this particular object on this particular spring;
F0·cos(ω·t) is an external periodic force acting on an object with the same angular frequency as an inherent natural angular frequency of oscillation of this particular object on this particular spring.
It's beneficial to represent A·cos(ω·t)+B·sin(ω·t) through a single trigonometric function as follows.
Let
D = √A²+B²
Angle φ is defined by
cos(φ) = A/D
sin(φ) = B/D
(on a Cartesian coordinate plane this angle is the one from the X-axis to a vector with coordinates
Then
A·cos(ω·t)+B·sin(ω·t) =
= D·[cos(φ)·cos(ω·t) +
+ sin(φ)·sin(ω·t)] =
= D·cos(ω·t−φ)
Now the general solution to our differential equation that describes forced oscillation looks like
x(t)=F0·t·sin(ω·t)/(2m·ω) +
+ D·cos(ω·t−φ)
where
F0 is an amplitude of a periodic external force;
m - mass of an object on a spring;
k - elasticity of a spring;
ω=√k/m is an inherent natural angular frequency of oscillation of this particular object on this particular spring and the angular frequency of external periodic force;
t is time;
D and φ parameters are determined by initial conditions for x(0) and x'(0).
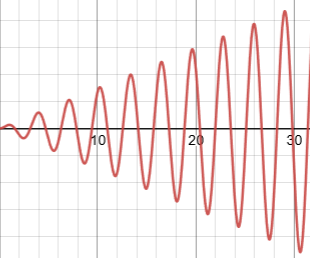
The main component of the function describing the movement of an object, when a periodic external force acts synchronously with the inherent natural oscillation of an object on a spring, is F0·t·sin(ω·t)/(2m·ω).
This function represents oscillation with gradually, proportionally to time t, increasing to infinity amplitude.
Added to this function is a regular sinusoidal oscillation with the same angular frequency but, potentially, a phase shift φ.
The periodic external force, acting synchronously (that is, with the same angular frequency) with inherent natural oscillation of an object on a spring, causes proportional to time increasing of an amplitude of oscillations to (theoretically) infinity. This is called the resonance.
Let's represent it graphically for some specific case of initial conditions and parameters.
Initial conditions:
x(0) = 0
x'(0) = 0
From these initial conditions follows
0 = D·cos(φ)
0 = D·ω·sin(φ)
We know that ω≠0.
Also, sin(φ) and cos(φ) cannot be simultaneously equal to 0.
Therefore, D=0, and our oscillation in this case is described by a function
x(t) = F0·t·sin(ω·t)/(2m·ω)
Parameters:
m=1
k=4
ω=√k/m=2
F0=12
With the above initial conditions and parameters the oscillation of the object is described by function
x(t)=12·t·sin(2t)/(2·1·2) = 3·t·sin(2t)
The graph of this function looks like this


No comments:
Post a Comment