Musical Strings 2
In the previous lecture we considered the model of a musical string as a point-mass m between two identical springs of the length (L+l)/2 each (where L is a neutral length of the string we are modeling and l is a stretch to create initial tension) with a coefficient of elasticity k.
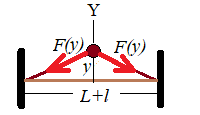
Plucking a string is, therefore, modeled as an initial displacement of a point-mass vertically by y(0)=a.
The result of the analysis of forces acting on a point-mass between these springs, when it performs transverse oscillations, was a differential equation
y"(t) + 2·(κ/m)·y(t)·
·[1−L/√(L+l)²+4y²(t)] = 0
Let's examine this model from the energy standpoint.
By lifting a point-mass initially by distance y(0)=a, we perform some work against elastic forces of two springs. The forces are variable and depend on how much we stretch the springs. Let's take coordinate y as our argument. Then, as explained in the previous lecture, the forces of two springs acting along the Y-axis against our motion total to
F↓↓(y) = −2·κ·y·
·[1 − (L/2) /√((L+l)/2)²+y²] =
= −2·κ·y·[1 − L /√(L+l)²+4y²]
Incidentally, it's easy to see that an expression in [...] is always positive, therefore the sign of the force is always opposite to the sign of a displacement y.
On an interval from y to y+dy of the infinitesimal length dy we can assume the constant force, as described above.
Therefore, the work we perform on that infinitesimal interval by going against the force F↓↓(y) is
dW = −F↓↓(y)·dy
We can now calculate the total work performed by displacing our point-mass by distance y(0)=a by integrating the above expression from y=0 to y=a.
W[0,a] = −∫[0,a]F↓↓(y)·dy =
= ∫[0,a]2·κ·y·
·[1−(L/2) /√((L+l)/2)²+y² ]·dy =
= ∫[0,a]2·κ·y·
·[1−L/√(L+l)²+4y² ]·dy
This integral can be calculated.
The answer is
W[0,a] = 2·κ·[y²/2 −
− (L/4)·√(L+l)²+4y² ] |[0,a] =
= 2·κ·[a²/2 −
− (L/4)·√(L+l)²+4a² +
+ L·(L+l)/4] =
= κ·[a² − (L/2)·√(L+l)²+4a² +
+ L·(L+l)/2]
Just to check, if a=0, the work performed is
W[0,0] =
= κ·[0² − (L/2)·√(L+l)²+0² +
+ L·(L+l)/2] = 0
as it is supposed to be.
Analysis of the potential energy W(a) as a function of the initial displacement a shows that it resembles the parabola with a graph like this:
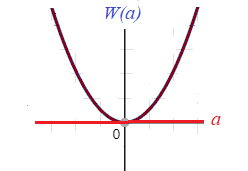
So, potential energy is always positive, as it should be, and grows with initial displacement a growing to positive or negative direction (up or down on a picture of a point-mass between two springs above).
At any displacement point y from the neutral position a point-mass m has certain potential and kinetic energy.
Its potential energy W(y), as a function of displacement y, looks exactly the same as the one we calculated at the initial position, when y=a, which yields
W(y) =
= κ·[y² − (L/2)·√(L+l)²+4y² +
+ L·(L+l)/2]
Obviously, this formula is valid only for
The difference between W[0,a] and W(y) is the kinetic energy our point-mass possesses because it moves towards the neutral position, that is
K(y)=m·(y')²/2.
Therefore, we have an equation, which is a differential equation for a displacement y(t) as a function of time t (in many cases we will drop (t) for brevity).
W(y) + K(y) = W[0,a]
The differential equation for displacement y(t) is
κ·[y² − (L/2)·√L+l)²+4y² +
+ L·(L+l)/2] + m·(y')²/2 =
= κ·[a² − (L/2)·√(L+l)²+4a² +
+ L·(L+l)/2]
Simplifying...
y² − (L/2)·√(L+l)²+4y² +
+ (m/κ)·(y')²/2 =
= a² − (L/2)·√(L+l)²+4a²
or
(m/2κ)·(y')² + y² −
− (L/2)·√(L+l)² + 4y² =
= a² − (L/2)·√(L+l)²+4a²
This is a different differential equation that describes the transverse oscillations of a point-mass between two springs than that described in the previous lecture.
It contains only the first derivative of a displacement y(t).
Interestingly, though not surprisingly, this equation is not really different.
If two functions are equal, their derivatives are also equal. Take a derivative from both sides of an equation above:
(m/2κ)·2y'·y" + 2y·y' −
− (L/2)·8y·y' /2√(L+l)² + 4y² =
= 0
or
(m/2κ)·y'·y" + y·y' −
− L·y·y' /√(L+l)² + 4y² =
= 0
Now we can cancel y'(t) getting
(m/2κ)·y" + y −
− L·y /√(L+l)² + 4y² = 0
or
(m/2κ)·y" + y·
·[1 − L /√(L+l)² + 4y²] = 0
or
y" + (2κ/m)·y·
·[1 − L /√(L+l)² + 4y²] = 0
which is exactly the same as the equation derived in the previous lecture.


No comments:
Post a Comment