Wave Equation 2
Let's approach transverse waves quantitatively. More precisely, we would like to express analytically the correspondence between different characteristics of ideal transverse waves -
time t,
period T,
angular frequency ω,
speed of propagation v,
amplitude A,
wave length λ and
wave number k.
We consider waves produced by harmonic oscillations of one end of an infinite rope, as on this picture:
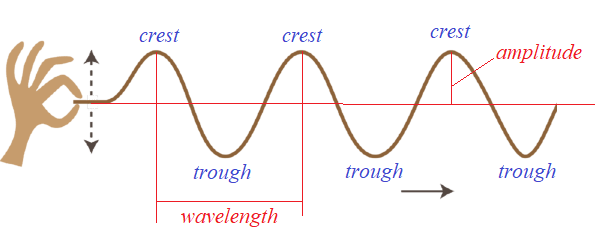
(open this picture in a new tab of your browser by clicking the right button of a mouse to better see details)
For the purpose of this lecture we will simplify the real oscillations of segments of a rope and assume that each its segment is moving only transversely (perpendicularly to a stretch of a rope) and repeats the harmonic oscillation of the rope's end that drives the oscillations.
As explained in the previous lecture, the essence of waves is that any subsequent segment of a rope repeats the motion of the previous segment, but with a time delay.
The delay depends on how far segments are from each other and on the speed of propagation of the waves v.
The speed of wave propagation, in turn, depends on many physical characteristics of a rope and is considered as given.
Let the X-axis be directed along the stretch of a rope, and
Then the
Assuming the initial position of the driving end of a rope is x=0 and y=0, its harmonic oscillations can be described as
y(t) = A·sin(ω·t)
where (in SI units)
y(t) - displacement (meters)
A - amplitude (meters)
ω - angular frequency (rad/sec)
t - time (sec)
For any other point on a rope the displacement (deviation from X-axis, oscillations, wave function) y() depends not only on time t, but also on a distance x from the rope's end that drives the oscillations, because the time delay of this point's motion relatively to motions of the rope's end depends on this distance. So, it's appropriate to analyze the function y(x,t) - a displacement of a point of a rope on a distance x from the rope's driving end at moment of time t.
In terms of the wave function y(x,t), the oscillations of the rope's end (x=0) are described as
y(0,t) = A·sin(ω·t)
The parameters that must be given to define the oscillations y(x,t) for any x and t are:
A - amplitude
ω - angular frequency and
v - wave propagation speed
The first two determine the oscillations of the driving end of a rope.
The wave propagation speed will help to define the oscillations of any other point on a rope.
Using these parameters, we can determine the wave function y(x,t) of any point of a rope.
As mentioned before, every point of a rope repeats the motions of the rope's driving end with a delay that depends on a distance between this point and the driving end of a rope x.
If the speed of wave propagation is v, the time delay will be x/v.
So, function y(x,t) should be equal to y(0,t−x/v).
Indeed, assume that at t=t0 the driving end of a rope is at
To have that same value at distance x from the rope's end at the time moment t0+x/v we have to set function y(x,t) to
y(x,t0) = y(0,t0−x/v)
Then
y(x,t0+x/v) = y(0,t−x/v+x/v) =
= y(0,t0)
which is exactly what we need - at t=t0+x/v - function y(x,t) equals to y(0,t0).
So, our final expression for a wave function that represents the Y-coordinate of a point at distance x from the rope's end at time t is
y(x,t) = y(0,t−x/v) =
= A·sin(ω·(t−x/v))
This form of wave equation can be transformed in many different ways, using different parameters and expressions of one parameter in terms of others.
Recall the following definitions.
The wave length λ is the distance between two consecutive wave crests or troughs.
The period T is the time a wave propagates by a distance equal to its wave length λ moving with its wave propagation speed v, that is T=λ/v.
On the other hand, if we consider a function sin(ω·t), it has a period ω times smaller than function sin(t). The latter has a period 2π. Therefore, function sin(ω·t) has a period T=2π/ω and, therefore, ω=2π/T=2π·v/λ.
The above formulas allow us to transform the obtained wave equation
y(x,t)=A·sin(ω·(t−x/v))
into
y(x,t) = A·sin(2π·(t−x/v)/T) =
= A·sin(2π·(t−x/v)·v/λ) =
= A·sin(2π·(v·t−x)/λ)
The quantity k=2π/λ is called wave number. From this definition follows that
k·v = (2π/λ)·(λ/T) = 2π/T = ω
This can be used in yet another form of the wave equation
y(x,t) = A·sin(k·(v·t−x)) =
= A·sin(ω·t−k·x))
From this we conclude that a point at distance x from the driving end of a rope performs the same oscillating motions as the rope's driving end, but shifted by phase equal to k·x, where k is a wave number.
All the above forms of the wave equation are equivalent to each other and are used interchangeably.
We have started with harmonic oscillations of a driving end of a rope as y(0,t)=A·sin(ω·t). It was based on initial position of the rope's end y(0,0) at
(not zero).
Another possibility would be to start from y(0,0)=A and no initial speed y'(0,0)=0.
To satisfy these initial conditions of the harmonic oscillations we can choose a function y(0,t)=A·cos(ω·t).
Then the wave equation takes a different form
y(x,t) = y(0,t−x/v) =
= A·cos(ω·(t−x/v)) =
= A·cos(2π·(t−x/v)/T) =
= A·cos(2π·(t−x/v)·v/λ) =
= A·cos(2π·(v·t−x)/λ) =
= A·cos(k·(v·t−x)) =
= A·cos(ω·t−k·x))
As you see, the general sinusoidal behavior is preserved in this case, as sine and cosine functions behave pretty much the same way with only difference in phase shift.
Finally, let us point again that the above analysis is based on a simplified model of transverse oscillations with every point along a rope performing harmonic oscillation, repeating the harmonic oscillations of a driving end of a rope with some time delay (or phase shift) that depends on wave propagation speed.
Reality, as usually, is much more complex than our models.


No comments:
Post a Comment