Problem 3: UNIZOR.COM - Physics4Teens - Waves - Mechanical Oscillations

Notes to a video lecture on http://www.unizor.com

Problems 3

Problem A


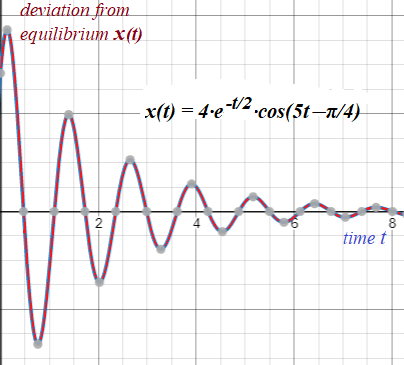
An object, oscillating in viscous environment, moves according to the following equation of motion
x(t) = 4·e^-t/2·cos(5t−π/4)
where t is time and x(t) is deviation from the equilibrium.

Determine the moments of time {t_i} = {t₀, t₁, t₂, ...}, when the object returns to the equilibrium.

Solution

Since we are talking about damping oscillations with diminishing displacements from the equilibrium, the motion is not exactly periodic, but we use the term period in a sense that an object returns to the equilibrium point again and again, albeit deviating from it less and less.

In this context period means the interval of time between consecutive crests or consecutive troughs of the trajectory, or between moments in time, when an object returns to the equilibrium position after reaching its local maximum deviation in both directions from the equilibrium.

Calculations below show that this interval does not change with time and remains constant, while the amplitude of oscillations around the equilibrium gets smaller with time.

To find the times when the object returns to the equilibrium, we have to find points, where x(t)=0.
Since coefficient in front of cos(...) never equals to zero, the solutions of an equation x(t)=0 are those moments in time, when cos(5t−π/4)=0.

Solving the equation:
cos(5t−π/4) = 0
5t−π/4 = π/2+N·π
5t = 3π/4+N·π
t = 3π/20+N·π/5
t = (3+4N)·π/20
where N ≥ 0 - an integer.

Interval between any two consecutive time moments of return to the equilibrium equals to π/5 (constant).
This makes a period of oscillation to be 2π/5 to allow an object to move from the equilibrium to one direction, return to the equilibrium, move to another direction and return again.

Substituting N=0,1,2..., we will get values {t₀=3π/20, t₁=7π/20, t₂=11π/20, ...}
The first few members of this sequence are
t₀ ≅ 0.471
t₁ ≅ 1.100
t₂ ≅ 1.728

Answer

{t_i} = (3+4N)·π/20
where N ≥ 0 - an integer.


Problem B

Consider the same object and environment as in Problem A.
Determine the moments of time {τ_i} = {τ₀, τ₁, τ₂, ...}, when the absolute value of object's deviation from the equilibrium reaches its local maximum.

Solution

Local extremes (maximum and minimum) of function x(t) are characterized by the fact that the derivative x'(t) at these points equals to zero.
x'(t) = −2·e^-t/2·cos(5t−π/4) −
− 20·e^-t/2·sin(5t−π/4) = 0

From this follows
cos(5t−π/4)+10·sin(5t−π/4)=0
tan(5t−π/4) = −1/10
5t−π/4 = arctan(−1/10) + N·π
5t = arctan(−1/10) +
+ (4N+1)·π/4
t = 0.2·arctan(−1/10) +
+ (4N+1)·π/20
where N ≥ 0 - an integer.

Since
arctan(−1/10) ≅ −0.0996686525,
the first few members (N=0,1,2) of this sequence are
τ₀ ≅ 0.137 (local max)
τ₁ ≅ 0.765 (local min)
τ₂ ≅ 1.394 (local max)

Answer

{τ_i} = 0.2·arctan(−1/10) +
+ (4N+1)·π/20
where N ≥ 0 - an integer.


Problem C

Determine the values of object's deviations from the equilibrium {A0, A1, A2, ...}, when they are at local maximums by absolute value.

Solution

A_i = x(τ_i)
Therefore, the first few members of this sequence are
A₀ ≅ 3.716 (local max)
A₁ ≅ −2.714 (local min)
A₂ ≅ 1.983 (local max)

Answer

{A_i} = {4·e^{τ_i·cos(5τ_i−π/4)}}
where values {τ_i} were determined in Problem B.