Convex Lenses
In this lecture we will use the material of the previous lecture "Prismatic Lenses" and strongly recommend to be familiar with its context.
Convex lenses serve to change the direction of rays of light (for example, coming from Sun) to produce images for some technical purpose (for example, to generate heat by focusing the Sun rays into one point).
Before discussing convex lenses, consider a case of a double-angled prismatic lens of the following section.
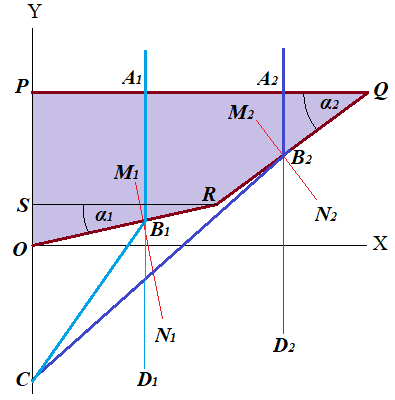
As in the previous lecture, we consider the light going from the medium with higher speed (like air) into a transparent prismatic lens made of a substance with a lower speed of light (like glass or silicon) and then refracted on the way out back into the air.
Assume two rays of light A1B1 and A2B2 fall perpendicularly onto the top surface PQ of this lens, continue on the same trajectory down without changing a direction (because they are perpendicular to the top surface) and are refracted by the bottom surfaces OR (for A1B1 refracted to B1C) and RQ (for A2B2 refracted to B2C).
Our goal is to find conditions on the shape of this prismatic lens and location of points A1 and A2 such that refracted rays intersect the Y-axis at the same point C, that we assume to be located at a distance f from the point O at the base of a lens.
Let distances PA1 and PA2 be, correspondingly, x1 and x2.
Let angles of deviation of the light be ∠CB1D1=δ1 (from A1B1 to B1C) and ∠CB2D2=δ2 (from A2B2 to B2C).
Then, according to the results of the previous lecture "Prismatic Lenses",
∠CB1D1 = δ1 =
= arcsin[(ni/nr)·sin(α1)] − α1
Analogously,
∠CB2D2 = δ2 =
= arcsin[(ni/nr)·sin(α2)] − α2
where
ni is the index of refraction of the medium of the incident ray of light and
nr is the index of refraction of the medium of the refracted ray of light.
All elements used in these formulas (indices of refraction and angles of the prism) are known, therefore angles of deviation are fully defined.
Let's determine the locations of points A1 and A2 to assure that refracted rays of light intersect the Y-axis at the same point C.
The length of segment OC=f.
Then, according to the results of the previous lecture "Prismatic Lenses", on one hand, considering the ray of light A1B1,
f = x1·[cot(δ1) − tan(α1)]
and, considering the second ray of light A2B2,
f = x2·[cot(δ2) − tan(α2)]
where the angles δ1 and δ2 were represented above in terms of α1 and α2 correspondingly.
As we see, the necessary condition for these two rays to come to the same point C on the Y-axis is the above formulas that combine the angle between the refracting bottom surface of a prism with the horizontal plane (α1 for OR and α2 for RQ) and the distance of the incoming ray of light from the Y-axis (x1 for PA1 and x2 for PA2).
The next step on the way to study convex lenses is to consider a multi-angled prismatic lens with set of rays of light falling perpendicularly to its top surface at points Ai with many refracting surfaces, one per each ray of light, each having its own angle with a horizontal plane αi.
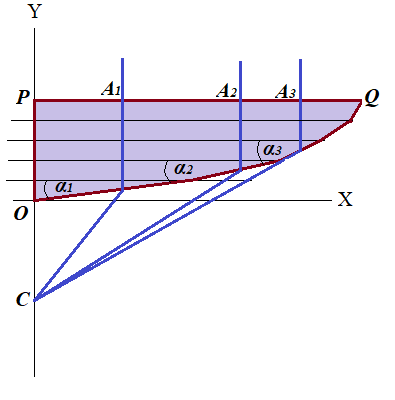
Now for each refracted ray of light we can use the same formulas as above to represent the dependency between
(a) the desired distance f,
(b) the distance xi=PAi of the falling light from the Y-axis,
(c) the angle αi between the corresponding refracting surface with a horizontal plane:
f = xi·[cot(δi) − tan(αi)]
where
δi = arcsin[(ni/nr)·sin(αi)] − αi
Consider now a convex lens that is a three-dimensional object obtained by a rotation of figure PQO around the Y-axis.
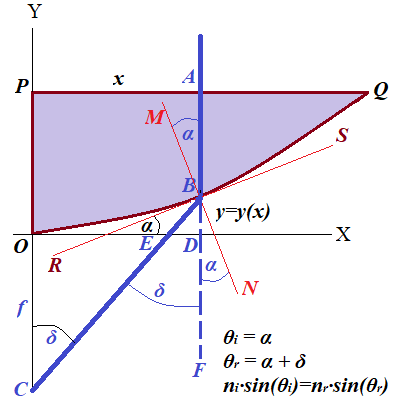
Line PQ is perpendicular to the Y-axis, curve OQ can be represented by some function y=y(x), which would be desirable to find, based on certain properties of a lens, which we need to have, primarily, its ability to concentrate the parallel rays of light falling perpendicularly to its top surface in one point on the Y-axis called the focal point.
Considering the symmetry, we can analyze the two-dimensional section of this lens formed by a plane going through the axis of rotation Y and any particular ray of light AB falling perpendicularly to PQ at a distance PA=x from the Y-axis.
All actions then will be occurring within this section plane.
The direction of a refracted ray of light BC can be obtained by
(a) drawing a tangential RS to curve OQ at the point of refraction B,
(b) drawing a normal to a surface of rotation at this point, which is a perpendicular MN to tangential RS and
(c) calculating the angle of refraction ∠CBN between the refracted light and a normal to a surface of refraction at point B.
Let's assume that curve OQ is a graphical representation of some function y=y(x), where x is a distance of the incident ray of light from the Y-axis.
If tangential RS makes an angle α with X-axis, the incident light makes the same angle α with a normal MN to a refracting surface at point of refraction B, because these two angles, ∠ABM and an angle formed by a tangential RS and X-axis, have correspondingly perpendicular sides.
If function y=y(x) represents curve OQ, the tangent of the angle tangential RS makes with X-axis is the first derivative of this function: tan(α) = y'(x)
Using the Law of Refraction, we determine the refraction angle ∠CBN:
ni·sin(α) = nr·sin(∠CBN)
A refraction angle ∠CBN can be viewed as a sum of two angles:
(a) a deviation angle ∠CBF=δ between the original direction of the light AB and the refracted ray BC and
(b) an angle ∠FBN that is equal to an incidence angle ∠ABM as vertical and, therefore, is equal to α
Putting all this information together, we can construct an equation that defines the refraction of the ray of light AB off the surface defined by a rotation of the curve OQ that we describe as a function y=y(x).
From triangle ΔOCE we can find OE=f·tan(δ).
From triangle ΔBDE we can find DE=y(x)·tan(δ).
Adding these two segments together, we obtain
OE+DE = x = [f+y(x)]·tan(δ)
Nice equation above, easily solvable for y(x), unfortunately, has an unknown angle δ. This angle should be determined based on the shape of curve OQ defined by function y=y(x) and the distance x of the incident light from the Y-axis.
We know that δ+α constitute the refraction angle, which in turn, can be obtained from the incidence angle and the Law of Refraction:
nr·sin(δ+α) = ni·sin(α)
This allows to find angle δ in terms of the incidence angle α:
sin(δ+α) = (ni/nr)·sin(α)
δ+α = arcsin[(ni/nr)·sin(α)]
δ = arcsin[(ni/nr)·sin(α)] − α
It's convenient to use relative index of refraction n=ni/nr to simplify the above as
δ = arcsin[n·sin(α)] − α
Also, recall that tangent of an angle from the X-axis to a tangential RS is the first derivative of function y(x).
Therefore, tan(α)=y'(x) and
α = arctan[y'(x)]
Summarizing all of the above, we have come to a differential equation for function y(x) that describes the shape of a bottom refracting surface of a lens that perfectly focuses all the rays of light falling perpendicularly onto its top flat surface into one focal point at a given focal distance f from the lens
x = [f+y(x)]·tan(δ)
where
δ = arcsin[n·sin(α)] − α and
α = arctan[y'(x)]
We deliberately didn't substitute δ and α to obtain one huge differential equation that contains only x, y(x) and y'(x) to preserve some readability.
The solution to this differential equation is not a circle, nor a parabola, nor hyperbola, nor exponent. It's much more complex. All the above elementary functions, when used in lenses, produce an effect called aberration, they do not concentrate all the rays of light going parallel to the Y-axis in one focal point.
There are numerical methods to approximate the solution to this differential equation.
Also, relatively recently the analytical solution to a more general problem with any top surface of a lens (like spherical) was obtained by young scientists in Mexico. Anyone interested can search for Wasserman-Wolf problem.


No comments:
Post a Comment