Prismatic Lenses
The main feature of the refraction of the light is the change of the direction of the ray of light after crossing from one transparent medium into another.
This feature is used in lenses to redirect the parallel rays of light.
This lecture is about right angle triangular prismatic lenses.
Specifically, we go through some calculations of the trajectory of light after it passes this type of a lens.
Consider a side section view of the right angle triangular prismatic lens with a ray of light falling perpendicularly to its side as on the following picture.
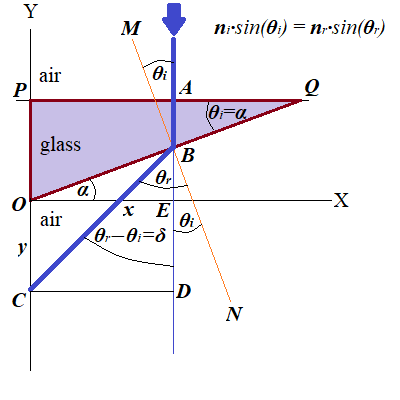
The ray of light (solid blue line on a picture above) entering a prism perpendicularly to its surface, goes through it without changing its direction (because it's perpendicular to a surface) and at the exit from a prism changes its direction, according to the Law of Refraction
ni·sin(θi) = ni·sin(θi)
where
indices i and r represent, correspondingly, incident and refracted rays of light,
ni is a refraction index of the air above and below the prism,
nr is a refraction index of the glass the prism is made of,
∠MBA = θi is the angle of incidence between incident ray of light and a normal MN to a surface of refraction,
∠CBN = θr is the angle of refraction between refracted ray of light and a normal MN to a surface of refraction.
Notice that refraction index of a medium is a ratio between the speed of light in vacuum to the speed of light in this medium. Its always greater than 1 because the speed of light in vacuum is its maximum possible speed. Also, the speed of light in glass is less than in the air, that's why the glass refraction index is greater than that of the air.
Assume, the light falls on the upper surface of the prism PQ at a distance PA=x from the Y-axis.
Our task is to determine the angle ∠CBD of the deviation of the light from the original trajectory and the distance OC=y, where point C is the intersection of the refracted ray of light with Y-axis.
Our first step is based on the fact that angle of incidence ∠MBA=θi equals to the angle of a prism ∠PQO=α as angles with mutually perpendicular sides, and, therefore, should be considered as given.
Also, angle ∠DBN equal to angle of incidence ∠MBA=θi as vertical.
That implies that the angle of deviation of the ray of light from its original direction ∠CBD equals to
∠CBD = ∠CBN − ∠DBN =
= θr − θi = θr − α = δ
Since angle of incidence θi is defined by the given prism's angle ∠PQO=α and the angle of refraction θr is related to the angle of incident through the Law of Refraction
ni·sin(θi) = nr·sin(θr)
we have a clear path to find the angle of deviation:
1. sin(θr) = (ni/nr)·sin(α)
2. θr = arcsin[(ni/nr)·sin(α)]
3. ∠CBD = δ =
= arcsin[(ni/nr)·sin(α)] − α
The last statement represents a dependency of the angle of light deviation δ from the angle α between top and bottom surfaces of a prism.
To determine the length of a segment y=OC, we see that
OC = BD − BE
From the right triangle ΔBDC we can express the length of segment BD:
BD = CD·cot(δ) = x·cot(δ)
From the right triangle ΔOBE we can express the length of segment BE:
BE = x·tan(α)
Therefore,
OC = x·cot(δ) − x·tan(α) =
= x·[cot(δ) − tan(α)]
We came to the results of our calculations.
1. The angle of deviation δ, as demonstrated above, depends on the given prism angle α and refraction indices of media the light goes through.
2. The length y of a segment between the point O (the edge of a prism) and an intersection of a ray of light, falling on the top of prism at distance x and, subsequently, refracted by another prism surface, from the Y-axis is
y = x·[cot(δ) − tan(α)]
where
α is a prism angle between the plane the original ray of light is perpendicularly falling on and the plane refracting this light,
δ is an angle of deviation of the refracted ray of light from its original trajectory.
As a conclusion, we observe that
(a) the angle of deviation δ of the refracted ray of light from its original trajectory depends only on the physical characteristics of a prism and surrounding environment (prism angle α and indices of refraction inside and outside of a prism),
(b) the distance y=OC from the edge of a prism to a point of intersection of the refracted light with Y-axis is proportional to a distance x of the incident ray of light from the Y-axis. The further from the Y-axis the trajectory of the incident ray of light goes - the further from the point O the refracted ray of light intersects this axis.
Prism does not gather the parallel rays of light falling perpendicularly to its surface into one point, but maintains their parallelism on a different trajectory.


No comments:
Post a Comment