Energy of Light
As was presented in the lectures "Electric Energy" and "Magnetic Energy" of a chapter "Energy of Waves" in this part of a course "Physics 4 Teens", electromagnetic field carries energy, electric and magnetic.
The density of the field's total energy PE+M(t,x,y,z) at any time t at any point {x,y,z} of this field can be expressed as a sum of electric energy density
PE(t,x,y,z) = ½ε·E²(t,x,y,z)
where E(t,x,y,z) represents the intensity of an electric field
and magnetic energy density
PM(t,x,y,z) = ½(1/μ)·B²(t,x,y,z)
where B(t,x,y,z) represents the intensity of a magnetic field.
Constants ε and μ in the above expressions stand, correspondingly, for electric permittivity and magnetic permeability of an electromagnetic field.
For our purposes we assume the light propagates in the vacuum, so ε=ε0 and μ=μ0.
So, the total energy density of electromagnetic field is
PE+M(t,x,y,z) =
= PE(t,x,y,z) + PM(t,x,y,z).
Light is an oscillating electromagnetic field. Therefore, light carries energy.
Let's evaluate the amount of energy in one wave length λ of a single light ray propagating in vacuum in the direction of the Z-axis with speed c with sinusoidal harmonic oscillations of field intensities.
Assume, electric field intensity oscillates around the X-axis, depending on time t and distance from the source of light z, according to a formula:
E=E(t,z)=E0·cos(ω(t−z/c)),
where E0 is an amplitude and
ω is an angular frequency of oscillations.
The magnetic field intensity synchronously oscillates around the Y-axis with the same angular frequency ω:
B=B(t,z)=B0·cos(ω(t−z/c)),
where B0 is its amplitude.
The expression inside a cos() function for both (electric and magnetic) components of an electromagnetic field represents the fact that a wave on a distance z from the origin is similar to the wave at the origin (that is, when z=0), but reaches location z with a time delay of z/c needed to reach that point with the speed of wave propagation c.
Then the electric field energy in one wave length of this ray is
WE = ∫0λ½ε0E²(t,z)dz
which, considering the expression for electric field intensity, is
(1/2)·ε0)∫0λE0²·cos²(ω(t−z/c))dz
Analogously, the magnetic field energy in one wave length of this ray is
WM = ∫0λB²(t,z)/(2μ0)dz
which, considering the expression for magnetic field intensity, is
(1/(2μ0))∫0λB0²·cos²(ω(t−z/c))dz
Let's calculate the common for these two expression integral
∫0λcos²(ω(t−z/c))dz
Then we will use it for calculation of WE and WM.
Substitute
u = ω(t−z/c))
z = c·t−(c/ω)·u
Then
du = −(ω/c)·dz
dz = −(c/ω)·du
We have to change the limits of integration for a new variable u:
if z=0, u=ωt,
if z=λ, u=ωt-(λω)/c.
Recall the following relationships between angular frequency ω, speed of light propagation c, wave length λ, period τ and frequency f, which were all discussed in the lecture "Rope Energy" of the chapter "Energy of Waves" in this part "Waves" of the course "Physics 4 Teens":
λ = c·τ
τ = 1/f
f = ω/(2π)
from which follows that
λ = c·τ = c/f = 2πc/ω
Therefore, upper limit of integration for variable u is
ωt−(λω)/c = ωt−2π.
With all the above substitutions integral
∫0λcos²(ω(t−z/c))dz
can be expressed in terms of variable u as
∫ωtωt−2π cos²(u)·(−(c/ω)·du) =
= (c/ω)∫ωtωt−2π cos²(u)·du
Using trigonometric formula
cos²(φ) = ½[cos(2φ)+1]
and standard integration techniques, the result of integration is
(c/ω)∫ωtωt−2π cos²(u)·du =
= π·c/ω
Based on the above, the energy of one wave length λ of a single ray of light is
Wλ = (1/2)(ε0πc/ω)·E0² +
+ (1/(2μ0))(πc/ω)·B0² =
= [π·c/(2ω)]·[ε0·E0²+(1/μ0)·B0²]
Let's evaluate the amount of energy falling on some surface of area A during time T from a set of synchronous monochromatic parallel rays of light (flat waves) that are directed perpendicular to this surface based on speed of light c and its angular frequency (that we perceive as color) ω, assuming the light is harmonic synchronous oscillations of an electromagnetic field with electric amplitude E0 and magnetic B0.
During time T on the flat surface area A falls perpendicularly to it all the energy of an electromagnetic field in the volume V=A·c·T
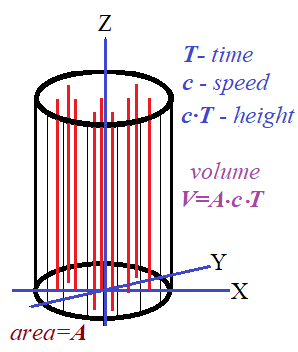
Assume that the direction of the propagation of light (red lines on the picture above) is vertically down along the Z-axis, while X- and Y-axes are on the bottom surface of area A.
The height of a cylinder on a picture above is the distance light covers in time T, that is, the height equals to c·T.
In this height we can fit certain number of wave length of waves. If the wave length is λ, the number of waves we can fit into the height c·T is
c·T/λ = c·T·ω/(2πc) = ω·T/(2π)
Taking into consideration the area A the light falls on, the total amount of energy falling on this area during time T is
WA,T = [ω·T·A/(2π)]·Wλ =
= [ω·T·A/(2π)]·
·[π·c/(2ω)]·[ε0·E0²+(1/μ0)·B0²] =
= [T·A·c/4]·[ε0E0² + (1/μ0)B0²]
Density of energy falling per unit of area per unit of time that can be called the average intensity of light I can be obtained by dividing the above expression by A and by T getting
I = [c/4]·[ε0E0² + (1/μ0)B0²]
An important addition to these calculations allows to express this average intensity of light only in terms of electric field intensity.
In the lecture "Speed of Light" of the chapter "Electromagnetic Field Waves" of this part of a course "Physics 4 Teens" we have derived a simplified form of the Fourth Maxwell Equation as
−∂By(t,z)/∂z = μ0·ε0·∂Ex(t,z)/∂t
where indices x under E and y under B correspond to a model we discuss in this lecture, that electric field intensity oscillates around X-axis, magnetic field intensity oscillates around Y-axis and the light propagates along Z-axis.
So, for our purposes we can safely drop these indices, which results in the following differential equation
−∂B(t,z)/∂z = μ0·ε0·∂E(t,z)/∂t
In that same lecture "Speed of Light" we have expressed the speed of propagation of electromagnetic waves in vacuum as
c² = 1/(μ0·ε0)
Using this, we can rewrite the differential equation with partial derivatives above as
−c²·∂B(t,z)/∂z = ∂E(t,z)/∂t
We have assumed that the ray of light is described by harmonic oscillations
E(t,z )= E0·cos(ω(t−z/c)),
B(t,z) = B0·cos(ω(t−z/c)),
Let's take the partial derivatives in the differential equation above for these field intensities.
∂B(t,z)/∂z =
= B0·sin(ω(t−z/c))·(ω/c)
∂E(t,z)/∂t =
= −E0·sin(ω(t−z/c))·ω
For these harmonic oscillations the differential equation above looks like
c·B0·sin(ω(t−z/c)) =
= E0·sin(ω(t−z/c))
from which follows
c·B0 = E0
Now the above expression for the amount of energy falling per unit of area per unit of time (average intensity of light) can be transformed into
I = [c/4]·[ε0E0² + (1/μ0)B0²] =
= [c/4]·[ε0E0² + (1/(c²·μ0))E0²]
From c²=1/(μ0·ε0) follows
that 1/(c²·μ0)=ε0.
Therefore,
I = [c/4]·[ε0E0² + ε0E0²] =
= c·E0²·ε0 /2
Simple transformations allow to express the same average intensity of light in terms of magnetic field intensity
I = c·B0²/(2μ0)
or in terms of both electric and magnetic field intensities
I = E0·B0/(2μ0)
An important consequence from the above formulas is that the density of light energy, that is the average amount of energy falling on a unit of area during a unit if time or average light intensity is proportional to a square of its amplitude.


No comments:
Post a Comment