Electrons
Electron is one of the three main particles present in every atom - protons and neutrons make up a nucleus, and electrons are rotating around a nucleus.
According to current view, electron is an elementary particle. Physicists have not identified any smaller particles that compose an electron.
There are some theories about some smaller particles inside an electron, but so far they have not been generally supported.
This leaves us to discuss the properties and characteristics of electrons, not their inner structure, like in the case of a proton or neutron with quarks and gluons they are composed of.
The first characteristic of an electron is its electric charge. When discussing subatomic particles, the electric charge of an electron is a unit of measurement. Therefore, its electric charge has absolute value of 1.
The electric field has two types of charge - positive and negative. An electron has a type negative, while a proton has type positive. Hence, we say that electric charge of an electron is −1, while a proton's electric charge is +1.
The usual symbol for an electron is e−.
Another important characteristic of an electron is its mass.
The experiments show that its mass is very small relatively to a mass of a proton or a neutron. In fact, it's almost 2000 times less than the mass of a proton.
We discussed the structure of an electron configuration of an atom in a lecture "UNIZOR.COM - Physics 4 Teens - Atoms - Electronic Structure of Atoms - Electrons and Shells" of this course. Let's continue this topic and get deeper into an electron configuration.
We know that electrons occupy shells around a nucleus, sequentially numbered 1, 2, 3 etc.
Every shell has certain number of subshells, and the number of subshells within each shell equals to a shell number:
shell #1 - 1 subshell s
shell #2 - 2 subshells s, p
shell #3 - 3 subshells s, p, d
shell #4 - 4 subshells s, p, d, f
etc.
Electrons within the same subshell have the same energy level.
There is another very important characteristic of an electron we have not discussed yet. It's called a spin.
An important property of an electron is that in the magnetic field it behaves like a little magnet similarly to a behavior of a electrically charged object spinning around an axis.
By analogy, physicists called this property of an electron a spin and, consequently, considered an orientation of the axis of this spin as an important characteristic of an electron.
A famous physicist Wolfgang Pauli suggested so called Pauli exclusion principle, according to which no more than two electrons can share a single trajectory (called orbital) within a subshell, and, if two of them do, they must have opposite orientation of the axis of their spins.
The number of orbitals inside a subshell depends on the subshell number. The first subshell s can have 1 orbital, the second subshell p has 3 orbitals, the third subshell d has 5 orbitals, etc. going along odd numbers, so subshell #X has 2X−1 orbitals.
Summarizing,
(a) electrons are moving within shells (#1, #2, #3 etc.)
(b) that are subdivided into subshells (a shell #N has N subshells with letters substituting the subshell numbers, like s for subshell #1, p for subshell #2, d for subshell #3 etc.)
(c) with 2M−1 orbitals inside a subshell #M
(d) where each orbital capable to hold no more than 2 electrons, which must have opposite spin.
We can represent this structure as the following table:
| Shell | Subshell | Orbits | # of e− |
| #1 | #1(s) | 1 | 2 |
| Σ(#1) | 1 | 2 | |
| #2 | #1(s) | 1 | 2 |
| #2 | #2(p) | 3 | 6 |
| Σ(#2) | 4 | 8 | |
| #3 | #1(s) | 1 | 2 |
| #3 | #2(p) | 3 | 6 |
| #3 | #3(d) | 5 | 10 |
| Σ(#3) | 9 | 18 | |
| #4 | #1(s) | 1 | 2 |
| #4 | #2(p) | 3 | 6 |
| #4 | #3(d) | 5 | 10 |
| #4 | #4(f) | 7 | 14 |
| Σ(#4) | 16 | 32 |
Simple calculations can prove that the number of orbits per shell #N equals to N² and, consequently, the maximum number of electrons that shell #N can hold is 2·N². This is exactly the formula obtained in the lecture "Electrons and Shells" referenced above.
Double Slit Experiment
There are many articles and videos about double slit experiment on the Web.
In particular, there is a lecture by Richard Feynman about it (almost an hour long).
More recently, Jim Al-Khlili did it in a more theatrical way in about 9 minutes, that I like a lot.
You can find both on the Web.
Below is yet another presentation of this topic, we do it for completeness of our story about electrons.
Imagine a box with two parallel slits at the bottom filled with sand. As sand goes down through slits it accumulates at the tray underneath a box forming two parallel hills, corresponding to two slits above the tray.
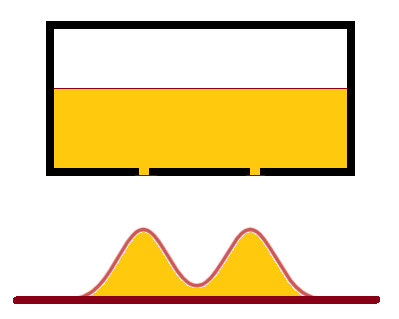
This is a clear example of how particles (in this case, sand) independently go through slits without interfering.
Consider an experiment with monochromatic light going through two slits. In this case the slits should be really close to each other and very narrow.
On a screen opposite to slits you will see the bright and dark lines - the result of interference between two rays coming through two slits.
Picture below reflects the intensity of light on a screen - a red curve with oscillating amplitude, maximum in the middle and diminishing to both ends.
Flat wave front of monochromatic light are split into two coherent rays. The bright and dark lines on a screen appear because these two rays come to a corresponding point on a screen in phase or out of phase. In the first case the interference between these rays is positive and enhance the brightness, in the second case rays work against each other and the spot is dark.
The lecture "UNIZOR.COM - Physics 4 Teens - Waves - Phenomena of Light - Interference" explains this process of interference in details.
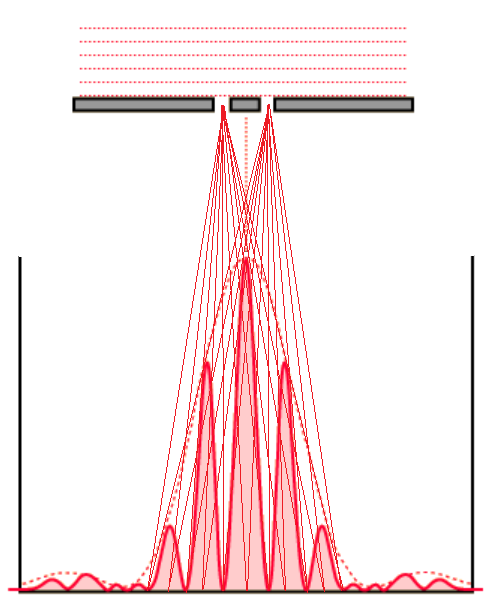
This is an example of how waves (in this case, waves of electromagnetic field) interfere with each other when going through two slits, making a completely different picture on a screen than if we dealt with particles, like sand above.
In these two experiments, we see two different behaviors of particles and waves going through two slits.
Particles going through different slits do not interfere with each other, while waves do.
Let's see how electrons behave in a similar setting.
Instead of flat wave front of monochromatic light we direct a bunch of electrons. Those that go through two slits will hit a screen with some sensitive to electron material, like the one used in old CRT computer screens.
What will we see on this screen?

Strangely enough, contrary to our perception that electrons are just small particles, the picture is as if electrons are waves that, going through two slits, interfere with each other.
Well, maybe, when a lot of electrons are going through slits, there are some forces among them that distribute them in such a pattern that resembles the interference.
Let's change the experiment and randomly send electrons one by one with sufficient time interval between them, so some will go through the first slit and some - through the second. This way they will not interfere with each other.
What will be a picture on a screen?
In the beginning we will see only individual dots randomly positioned on a screen. After sufficiently large number of electrons fall onto a screen, the pattern will be obvious, and it will be identical to the above pattern of interference.

Common sense tells us that, since electrons are sent to slits one at a time and they randomly go through one or another slit, there should be no information transfer from one electron to another and, therefore, no interference. We should just see two parallel lines on a screen, each across a corresponding slit, similarly to how sand goes through two slits. Yet, the picture was obviously like an interference.
Let's try to analyze which slit each electron goes through. Maybe, this will clarify the situation.
We put a detector near one slit that detects the electron passing by, and repeat the experiment with sending electrons to slits one at a time.
Indeed, about have the times our detector reacted on a passing by electron, as we would expect, considering the randomness of shooting electrons.
But to our surprise the picture on a screen now will be exactly as if individual particles hit slits and accumulate exactly opposite to slits on a screen. Indeed, a particle-like behavior.

That is strange. Do electrons see our detection device and change the behavior?
Let's fool the electrons. Since our detector of electrons requires some electricity to work, we will retain it in place, but unplug it from the wall.
Surprisingly, we will see the interference picture again.

Go figure.
That completes this pseudo-detective story about behavior of electrons going through a two slits configuration.


No comments:
Post a Comment