Logic 02
Problem A
The game starts with two sets of stones and two players.
At each turn a player can take any number of stones but only from one of the sets.
The winner is the player who takes the last stones.
The player who should start the game can yield this right of the first move to his opponent. After that to take some stones on each move is the rule.
What is the winning strategy for a person who starts the game?
Solution A
The strategy to win for the first player is on every move to equalize the number of stones in two sets.
If the initial number of stones is different in these two sets, the first move of the player who starts the game is to take a few stones from a bigger set to equalize the number of stones.
His opponent, always facing two equal numbers of stones in two sets, cannot take the last stone and inevitably will make the number of stones in two sets different.
If in the beginning the numbers of stones in these two sets are equal, the player who starts the game should yield the right of the first move to his opponent, achieving the same conditions as above.
Problem B
There is a set of six points, no three points of this set lie on a straight line.
For clarity we can assume that they lie on a circle, though it's not essential.
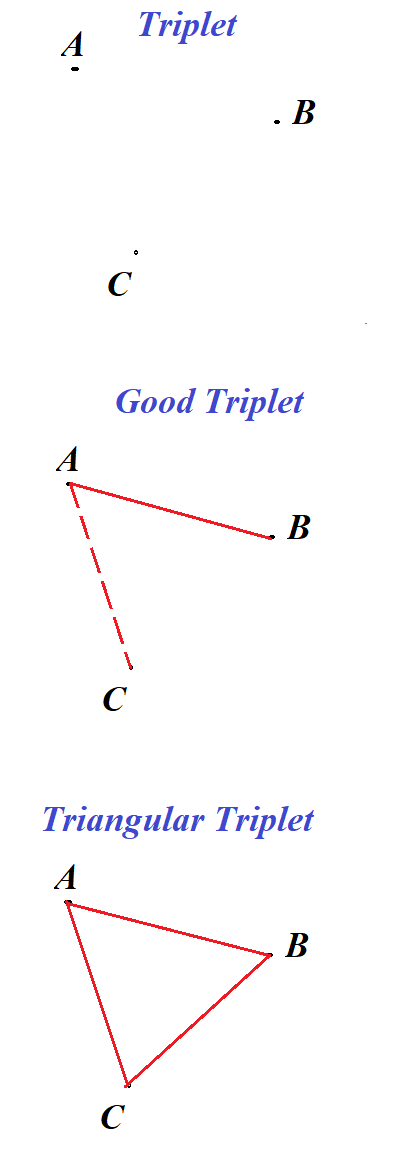
Consider all subsets of three points of this set of six (we will call these subsets triplets).
Let's call a triplet, that has one or more segments connecting its points, a good triplet.
If all three points of a good triplet are connected by three segments, we will call this triplet a triangle.
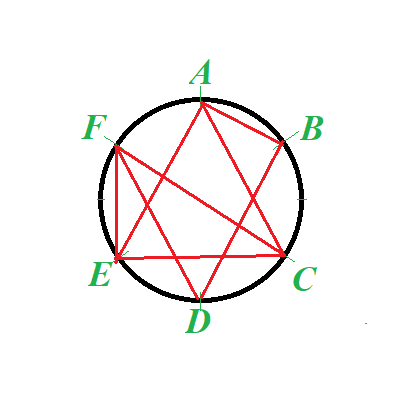
For example, on the picture below all triplets have at least one pair connected by a segment (triplet ABC has two segments AB and AC, triplet CDF has two segments CF and DF, triplet ABF has one segment AB etc.)
Let's try to connect some points with segments in such a way that in any triplet there would be a pair of points connected by a segment.
That is, let's try to make all triplets good.
Prove that, no matter how we try to accomplish this task of making all triplets good by connecting our six points, there would inevitably be a triplet with three segments connecting all its three points into a triangle (that is, there will be at least one triangle), like ΔACE or ΔCEF in the example above.
Solution B
First, let's prove the following auxiliary statement (lemma) using the following illustration.
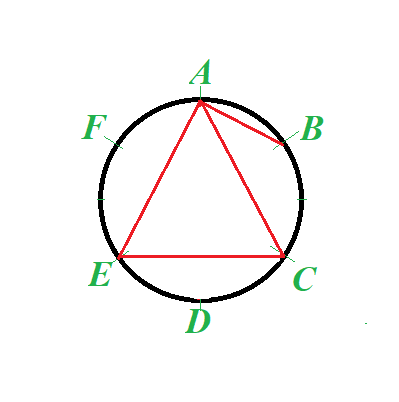
Assume that all triplets are good (as assumed in the Problem B) and some point (for example, A on the picture above) has three segments joining at it and connecting it to three other points (like on the picture above, point A is connected to B, C and E).
Then there exist a triangle.
Proof:
Since a triplet of three connected points (BCE on the picture above) is, as all other triplets, assumed to be good, there exists an additional connecting segment between some of its points (between C and E on the picture above).
With three given segments going from a point with three connections (AB, AC and AE on the picture above) and one additional segment between some connected points (segment CE between C and E on the picture above), there is a triplet (in our example it is ACD) that forms a triangle.
Consequently, to prove that in the process of connecting pairs of points to make all triplets good there would eventually have to be formed a triangle, it's sufficient to prove that there would eventually have to be a point with three segments connecting it to other three points.
The plan is to
(1) count all the triplets that can be formed from the given six points and
(2) show that without connecting three points into a triangle or connecting some point to three others (which, as lemma above proved, leads to forming a triangle) it's impossible to make all counted in (1) triplets good.
The total number of triplets is, obviously, the number of combinations of our six points in groups of three, which is
C63 = 6!/(3!·3!) = 20
Now let's proceed to make all triplets good, but obeying the rule of having no more than two segments joining at any single point (since, as we have proved, when three segments join in one point, triangle is unavoidable).
We have to make 20 good triplets, but we will show that we cannot make more than 18 without breaking that rule, which would necessitate the existence of a point with three segments connecting it to three other points, which is sufficient condition for existence of a triangle.
Let's start the process of connecting pairs of points to make good triplets.
In the beginning there are no connecting segments, so we choose any two points (call them A and B) and connect them with a segment.
This is sufficient to make 4 new good triplets: ABC, ABD, ABE and ABF.

Now we have a choice of which points to connect next.
We can either
(a) choose a pair of new points to connect by a segment (for example, D and E) or
(b) choose one new (unconnected) point and one that already has a connecting segment (for example, B and C), or
(c) choose two points that already had connecting segments, which could happen on later steps.
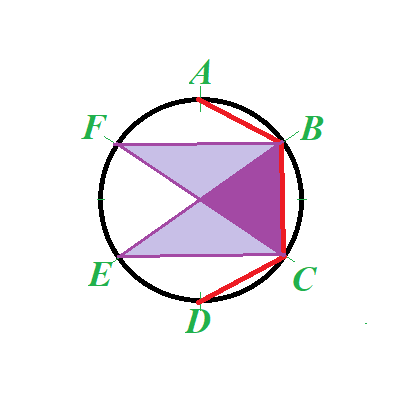
In case (a) we have 4 more good triplets (DEA, DEB, DEC and DEF in our example).
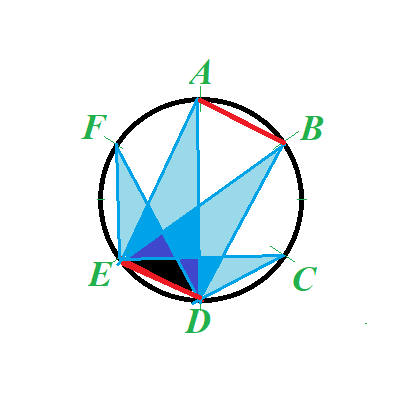
In case (b) only 3 good triplets will be formed (BCD, BCE and BCF in our example).
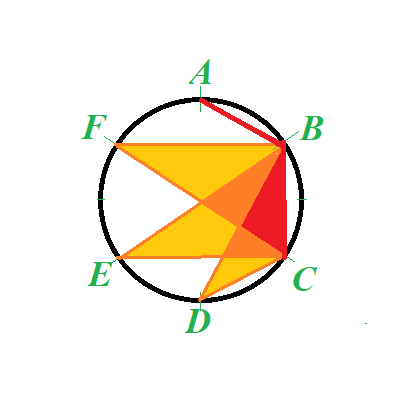
In case (c) only 2 good triplets will be formed (if segments AB and CD exist, and we connect points B and C with a segment, new good triplets BCE and BCF are formed).
General consideration is that the more segments connect our six points - the more good triplets will be formed.
Let's start with the strategy that assures the maximum number of segments - the one when there are two segments joining at each point, so the rule of not having three segments at any point is preserved.
This can be accomplished if all points are connected into a closed chain:
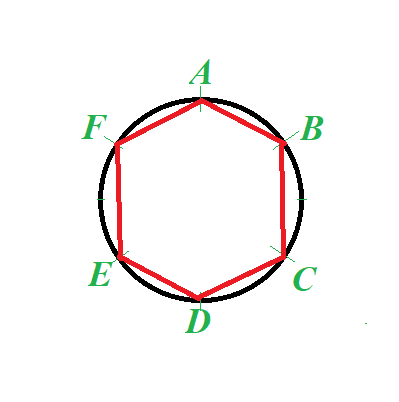
Obviously, not all triplets are good in this case. For example, ACE or BDF.
Another chained connection
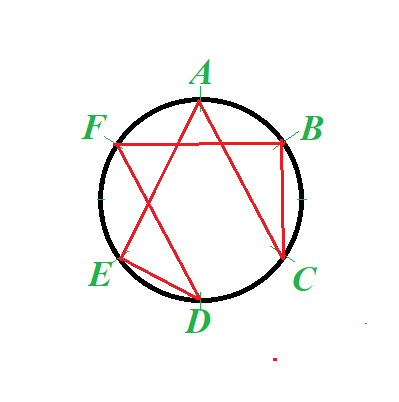
Here triplets ABD or CEF are not good.
Let's count good triplets using the first example of a chained connection above, starting from segment AB and moving clockwise (the order is unimportant, we can connect A-C-B-F-D-E-A, as exemplified on the second picture, and the result will be the same).
Segment AB, being the first, produced 4 good triplets, as was stated above.
Then four consecutive segments BC, CD, DE and EF formed 3 good triplets each.
Final segment FA added 2 more good triplets.
The total number of good triplets is
4+3+3+3+3+2=18
which is short of required 20, which means, to make all triplets good, we need more segments, which will result in some points to be connected by three segments to three other points and forming of a triangle will be guaranteed.
We can try to organize connections differently. Instead of putting all 6 points into a chain, we can do it with only 5 with points A-B-C-D-E, leaving point F outside.
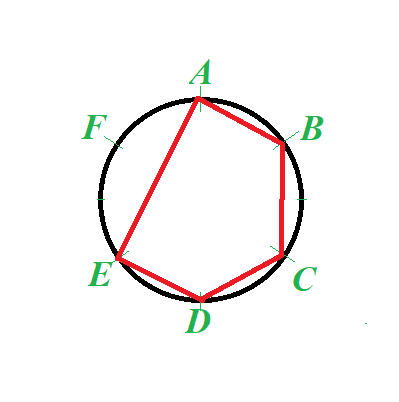
Similar counting of good triplets will result in the following:
Segments AB, as before, created 4 good triplets.
Segments BC, CD, DE, as before, created 3 good triplets each.
Finally, segment EA created two new good triplets: EAC and EAF.
The total number of good triplets is:
4+3+3+3+2 = 15
The last case is to leave two points out of a closed chain as follows.
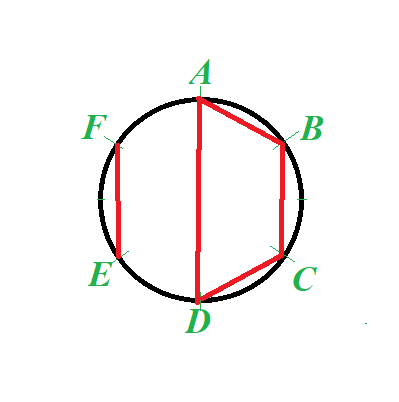
In this case the number of good triplets is:
from AB - 4,
from BC - 3,
from CD - 3,
from DA - 2 (DAE, DAF),
from EF - 4 (EFA, EFB, EFC, EFD)
The total number of good triplets is:
4+3+3+2+4 = 16
Still less than 20.
There are no logically different cases of connecting the points deserving a consideration, so we came to
CONCLUSION:
to have all 20 triplets as good, we need more that two segments joining at each point; it is impossible to avoid triangles.


No comments:
Post a Comment