Geometry+ 01
Problem A
Can two sides and all angles of one triangle be equal to two sides and angles of another triangle, but triangles be different (that is, not congruent because the third sides of these triangles have different lengths)?
If yes, are there any requirements on the sides of a triangle to assure the existence of a non-congruent to it another triangle with the same three angles and two sides?
Solution
Here is an approximate picture that seems to illustrate that this is possible.
Both triangles (red and blue) have the same angles α, β and γ and two equal sides a=a and b=b.
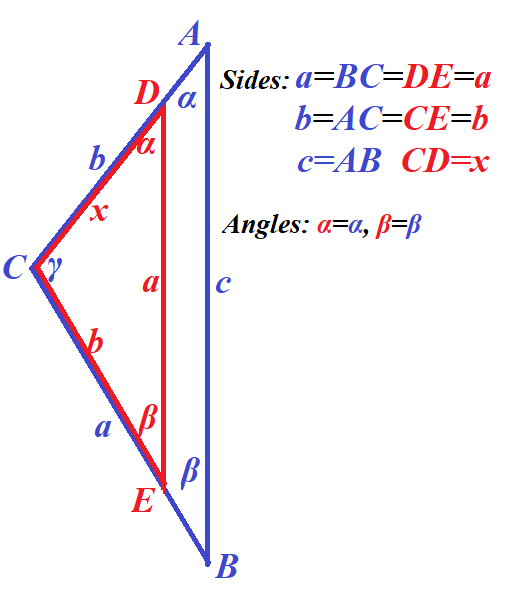
Point D lies on the segment AC.
Point E lies on the segment BC.
The length of segment BC=a is greater than the length of segment CE=b.
Sides are parallel: AB || DE
⇒ ∠CAB=∠CDE = α
⇒ ∠ABC=∠DEC = β
Therefore, triangles are similar:
ΔABC ∼ ΔDEC
Congruent sides:
BC ≅ DE = a
AC ≅ CE = b
Now the question is, can we start with any triangle ΔABC and construct ΔDEC that is similar but not congruent to ΔABC.
The answer is negative, we cannot start with any triangle ΔABC, but under certain conditions it is possible, and we will examine specific requirements to make it.
Let's assume that ΔABC is defined by its three sides BC=a, AC=b and AB=c.
Triangle ΔDEC is similar to ΔABC and we know its two sides - DE=a and CE=b.
Assume, the third side of ΔDEC is CD=x.
From similarity of these triangles follows that the ratio of sides lying opposite to equal angles is the same:
CB/CE = CA/CD = AB/DE
Therefore,
a/b = b/x = c/a
From the first equation follows that
x = b²/a
From the second equation follows that
x = a·b/c
Therefore,
b²/a = x = a·b/c
⇒ a²b = b²c
⇒ a² = b·c
The last equation a²=b·c is the necessary condition required to construct triangle ΔDEC.
As we stated above, length a is greater than b. Therefore, to satisfy the last equation, length c must be greater than a, that is, a is somewhere in-between b and c.
The condition a² = b·c with length a being somewhere between unequal b and c is also a sufficient one for the task.
To prove it, assume that we have triangle ΔABC with unequal sides a, b and c, as on the picture above, that satisfy the condition a² = b·c.
Using length b of side AC, we mark point E on the side BC at distance b=b from point C.
Next we draw a line parallel to AB through point E that crosses AC at point D.
Consider triangle ΔDEC.
All its angles are, correspondingly, congruent to angles of triangle ΔABC, so these triangles are similar.
Let's prove that the length of side DE equals to the length of side BC=a. That will conclude the construction (and, therefore, existence) of a triangle with two sides and all angles equal to two sides and all angles of triangle ΔABC, but not congruent to it.
Let the length of side DE be an unknown y.
From similarity of two triangle follows:
a/b = c/y
⇒ y = b·c/a
As we know, b=b and, by assumption, a²=b·c.
Therefore,
y = a²/a = a
which is exactly what we had to prove.
Conclusion
There might exist a triangle with two sides and all angles equal to two sides and angles of a given triangle and not congruent it, but there is certain necessary and sufficient condition for its existence in terms of an equation between the sides a,b,c of a given triangle.
Namely, all sides a,b,c must be different and they must satisfy an equation a²=b·c.
Example
Consider a triangle with sides a=6, b=4 and c=9.
It satisfies the conditions above (all sides are different and 6²=4·9).
Now we know two sides of a triangle we have to construct: a=6 and b=4.
The third side x can be found from the similarity condition
x/b = b/a
⇒ x = b·b/a = 16/6 = 8/3
To prove similarity, let's check the proportionality of all sides.
(8/3)/4 = 2/3
4/6 = 2/3
6/9 = 2/3
Angle Restriction
An interesting restriction can be derived on the value of angle ∠α lying between the longest and the shortest sides of triangle ΔABC across side a.
As we agreed, to make possible the existence of triangle ΔDEC with two (but not all three) sides and all three angles equal to those of ΔABC, the necessary and sufficient condition is
a² = b·c
At the same time, by the law of cosines,
a² = b² + c² −2b·c·cos(α)
Therefore, we have an equality
b·c = b² + c² −2b·c·cos(α)
or
2b·c·cos(α) = b² + c² − b·c =
= (b − c)² + b·c
Since (b−c)² is always positive, we conclude that
2b·c·cos(α) > b·c
or
cos(α) > ½
α < π/3 = 60°
Angle between the longest and the shortest sides of ΔABC should be less than π/3=60°.


No comments:
Post a Comment