Geometry+ 03: UNIZOR.COM - Math+ & Problems - Geometry

Notes to a video lecture on http://www.unizor.com

Geometry+ 03


This lecture is dedicated to problems of triangle construction by its certain elements.

The tools of construction are a ruler to draw straight lines and a compass to draw circles.

We will use the following naming rules.
Vertices of triangle will be call by upper case Latin letters A, B and C.
Sides will be called by lower case Latin letters corresponding to opposite vertices: side a is opposite to vertex A etc.
Angles will be called by lower case Greek letters corresponding to names of their vertices: angle α is at vertex A etc.
Medians are named m with a subscript of a side onto which they fall: median m_a is from vertex A to side a etc.
Altitudes are named h with similar subscripts, like h_a etc.
Angle bisectors are named l_a etc.
Radius of a circumscribed circle of a triangle is named R.
Radius of an inscribed circle is named r.

Problem A
Construct a triangle by its three altitudes h_a, h_b and h_c.

Analysis A

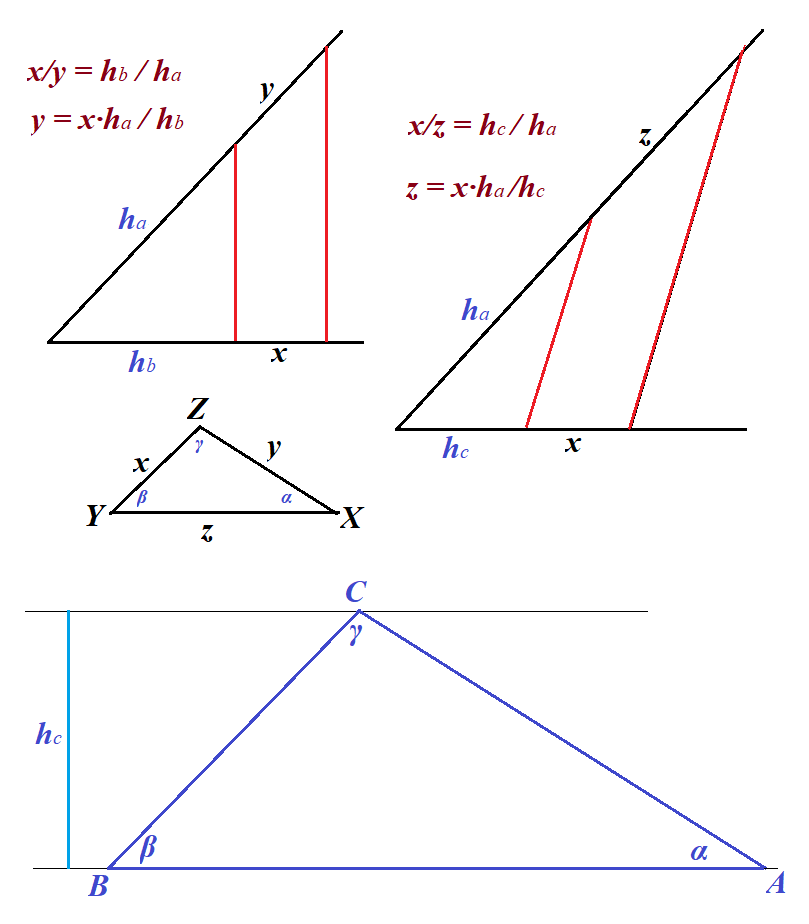
As we know, a product of a side by an altitude falling on it is a double area of a triangle.
Therefore,
a·h_a = b·h_b = c·h_c
Hence,
b = a·h_a/h_b
c = a·h_a/h_c

Let's construct a triangle similar to ΔABC defined by sides a, b and c by choosing any segment x and defining two other segments y and z using the equations similar to above.
y ≝ x·h_a/h_b
z ≝ x·h_a/h_c
Segments y and z can be easily constructed from these definitions, knowing x (arbitrarily chosen) and given altitudes.

Let x/a=k be a scaling factor between arbitrarily chosen segment x and side a of triangle ΔABC.
From this follow these relationships:
x = a·k
y = x·h_a/h_b = a·k·h_a/h_b = b·k
z = x·h_a/h_c = a·k·h_a/h_c = c·k
The scaling factor k is the same for x/a=k, y/b=k and z/c=k.

Therefore, triangle ΔXYZ constructed from three segments x, y and z is similar to triangle ΔABC with segments a, b and c we have to construct.

From similarity of triangles follows the congruence of corresponding angles
∠BAC = ∠α = ∠YXZ
∠CBA = ∠β = ∠ZYX
∠ACB = ∠γ = ∠XZY

Therefore, our analysis shows that by constructing ΔXYZ we get all angles of ΔABC.

This is the end of analysis, as the construction of triangle ΔABC, knowing its three angles and altitudes, is straight forward.

Solution A

To enlarge this picture, right click on it and choose "Open image in new tab"