Algebra+ 01: UNIZOR.COM - Math+ & Problems - Algebra

Notes to a video lecture on http://www.unizor.com

Algebra+ 01


Problem A

Given an equation of parabola in Cartesian coordinates on a plane
y = x² − A·x + A
where parameter A can be any real number.
Each value of parameter A defines some parabola.

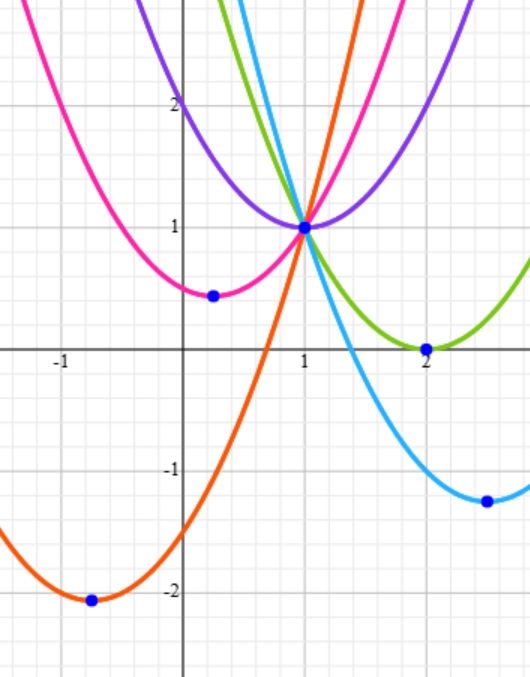
(A1) Find the point on a plane, through which go all the parabolas defined by all real values of parameter A.

(A2) On what curve lie the vertices of all the parabolas defined by all real values of parameter A?

Solution A

A1
Assuming the statement of this problem implies that such a point, where all parabolas are crossing, exists, let's find it by equating any two values of y for different values of parameter A.

Take, for example two parabolas for A=0 and A=1 and find their crosing point, that is such x for which corresponding quadratic forms equal to each other.
A=0 ⇒ y = x²
A=1 ⇒ y = x² − x + 1

Equating both expressions gives
x² = x² − x + 1
⇒ x = 1

Consider now this value x=1.
With this x the equation becomes independent of parameter A:
y = 1² − A·1 + A = 1
for any value of parameter A.

Therefore, any parabola defined by any value of A goes through point with coordinates x=1, y=1 on a plane.


A2
We need a formula for a vertex of a parabola represented by a general quadratic form
y = a·x² + b·x + c
If we do not remember the formula for X-coordinate of its vertex, recall that it is in the middle between the two roots of a quadratic equations
a·x² + b·x + c = 0
The formula for its roots (and that is something to remember) is
x_1,2 = [−b ± √b²−4ac] /2a
Therefore, the X-coordinate of a vertex is in the middle between its roots
x₀ = ½(x₁ + x₂) = −b/2a

Alternatively, using Calculus, we can find x₀ by equating a derivative of a given quadratic form to zero:
y' = 2ax + b = 0
Therefore,
x₀ = −b/2a

The Y-coordinate of a vertex is, therefore,
y₀ = a·x₀² + b·x₀ + c =
= a(b/2a)² + b(−b/2a) + c =
= b²/4a − b²/2a +c =
= −b²/4a + c

In our case of a quadratic form
y = x² − A·x + A
the values of coefficients are
a = 1, b = −A, c = A
Therefore, the coordinates of a parabola's vertex for a specific value of parameter A is
x₀ = A/2
y₀ = −A²/4 + A
As parameter A changes, so do coordinates of a vertex forming some parametrically defined curve.

To convert this parametric definition of a curve into the usual format y₀=f(x₀) we resolve parameter A in terms of x₀ and substitute it into an expression for y₀.
Since
x₀ = A/2
the value of A in terms of x₀ is
A = 2x₀

Substitute it into an expression for y₀:
y₀ = −4x₀²/4 + 2x₀ =
= −x₀² + 2x₀
which is a parabola with coefficients
a = −1
b = 2
c = 0

The standard characteristics of this parabola are as follows.
The "horns" are directed downwards.
Vertex is at
x₀ = −b/2a = −2/−2 = 1
y₀ = −b²/4a + c = −4/−4 + 0 = 1
Roots (X-intercepts) are
x_1,2 = (−2±√4)/−2
⇒ x₁ = 0, x₂ = 2