Algebra+ 02: UNIZOR.COM - Math+ & Problems - Algebra

Notes to a video lecture on http://www.unizor.com

Algebra+ 02


Problem

Let {x_i} (where i∈[1,n] and n is any natural number) be a set of n real non-negative numbers.

Their arithmetic average
(or mean) is defined as
A_n = (1/n)·Σ_i∈[1,n] x_i
(symbol Σ_i∈[1,n] is summation for all indices i∈[1,n])

Their geometric average is defined as
G_n = (Π_i∈[1,n] x_i)^1/n
(symbol Π_i∈[1,n] is multiplication for all indices i∈[1,n])

Prove that A_n ≥ G_n.

Solution A
(by Cauchy)

Our plan is multi-step.
First (step 1), we will check our inequality for n=1 and prove it for n=2.
Then (step 2) we will prove that, if it's held for some n, it will be held for 2n, which, if start with n=2 would prove the inequality for n=4, n=8 etc. - for all n=2^k, where k is any natural number.
Finally (step 3), we will prove for all other n by complementing any given n non-negative numbers {x_i} with some new numbers to make the total quantity of numbers equal to 2^k.

Step 1
It's obvious that for n=1 the inequality is held because
A₁ = x₁/1 = x₁
and
G₁ = (x₁)¹ = x₁

For n=2 let's prove it as follows.
Start from the original inequality that needs to be proven, do some reversible invariant transformations to get to an unconditionally true statement (this is the analysis stage) and then use the reversibility of invariant transformations to prove the original inequality by going backward through these transformations, beginning with final unconditionally true statement (the proof proper).

Note that all our participating numbers are real non-negative, it's important when we talk about reversible invariant transformations that involve raising both sides of inequality to the power of 2.

Original inequality to be proven:
(I) (x₁+x₂)/2 ≥ (x₁·x₂)^½
Now do the following series of invariant transformations.
(II) Square both sides (it is an invariant reversible transformation for non-negative numbers).
(x₁+x₂)²/4 ≥ x₁·x₂
(III) Open parenthesis.
x₁²+2·x₁·x₂+x₂² ≥ 4·x₁·x₂
(IV) Bring all members to the left side.
x₁² − 2·x₁·x₂ + x₂² ≥ 0
(V) Notice, we have a full square on the left, let's transform it into an explicit square:
(x₁ − x₂)² ≥ 0
The above is an unconditionally true statement.

Therefore, the above analysis allows us to formulate the proof by starting from this unconditionally true statement (V) and invariantly transform it into (IV), (III), (II) and (I), which proves the original inequality.
Step 1 of the proof is done.

Step 2
Let's prove that the quantity of non-negative numbers participating in arithmetic and geometric averaging can be doubled.
More precisely, we will prove that if the inequality is true for n elements, it's true for 2n elements.

Assume, A_n ≥ G_n for some n.
Let's prove that A_2n ≥ G_2n.
Divide our set of 2n elements into two subsets:
subset #1 {x_i}_i∈[1,n] and
subset #2 {x_i}_i∈[n+1,2n]

Let A_n⁽¹⁾ and G_n⁽¹⁾ be arithmetic and geometric averages of the elements of subset #1 and
A_n⁽²⁾ and G_n⁽²⁾ be arithmetic and geometric averages of the elements of subset #2.
Let A_2n and G_2n be arithmetic and geometric averages of the elements of an entire set of 2n elements.

Each subset contains n elements (non-negative numbers), and we assumed that our original inequality is held for this quantity of elements.
Therefore,
A_n⁽¹⁾ ≥ G_n⁽¹⁾ and
A_n⁽²⁾ ≥ G_n⁽²⁾.

Obviously,
A_2n = [A_n⁽¹⁾+A_n⁽²⁾] /2
G_2n = [G_n⁽¹⁾·G_n⁽²⁾]^½

Using the above assumption about inequality between arithmetic and geometric averages of sets of n elements,
A_2n = [A_n⁽¹⁾+A_n⁽²⁾] /2 ≥
≥ [G_n⁽¹⁾+G_n⁽²⁾] /2
Using the proven above inequality for only two elements G_n⁽¹⁾ and G_n⁽²⁾, we can state
[G_n⁽¹⁾+G_n⁽²⁾] /2 ≥
≥ [G_n⁽¹⁾·G_n⁽²⁾]^½ = G_2n

Combination of the two inequalities obtained above proves that
A_2n ≥ G_2n
Step 2 of the proof is done, and we can state that, since the inequality was proven for n=2, it is true for n=4,8,16..., that is for any n=2^k.

Step 3
Let's prove the inequality for values of n between powers of 2.
Let the value of n be greater than 2^k−1 but less than 2^k.
A_n and G_n are, as before, arithmetic and geometric averages of our n numbers.

Let's complement our set of n numbers {x_i}_i∈[1,n] with m=2^k−n new numbers, each of which is equal to G_n.
Now we have a set of 2^k=m+n numbers, and we can apply the inequality between arithmetic and geometric averages proven to be true for such sets.

Consider A_m+n for our new set that contains n original elements {x_i} and m new elements, each of which equals to G_n.
Obviously,
A_m+n = [n·A_n + m·G_n] /(m+n)

Now calculate G_m+n for our new set that contains n original elements {x_i} and m new elements, each of which equals to G_n.
Obviously,
G_m+n = [G_nⁿ · G_n^m]^1/(m+n) =
= [G_n^m+n]^1/(m+n) = G_n

Since m+n=2^k and our original inequality was proven for this quantity of participating non-negative numbers,
A_m+n ≥ G_m+n
Therefore,
[n·A_n + m·G_n] /(m+n) ≥ G_n

Simple transformations of the last inequality result in the following.
n·A_n + m·G_n ≥ (m+n)·G_n
n·A_n ≥ n·G_n
A_n ≥ G_n
Step 3 of the proof is done, and we can state that it was proven for any set of non-negative numbers that their arithmetic average is greater or equal to their geometric average.

Alternate step 3
Instead of complementing our original set of n numbers with G_n, we can complement it with A_n with similar results.
Then,
A_m+n = [n·A_n+m·A_n] /(m+n) =
= A_n

Now calculate G_m+n for our new set that contains n original elements {x_i} and m new elements, each of which equals to A_n.
G_m+n = [G_nⁿ · A_n^m]^1/(m+n)

Since m+n=2^k and our original inequality was proven for this quantity of participating non-negative numbers,
A_m+n ≥ G_m+n
Therefore,
A_n ≥ [G_nⁿ · A_n^m]^1/(m+n)

Simple transformations of the last inequality result in the following.
A_n^m+n ≥ G_nⁿ·A_n^m
A_n^m·A_nⁿ ≥ G_nⁿ·A_n^m
A_nⁿ ≥ G_nⁿ
A_n ≥ G_n

The equality between arithmetic and geometric averages is obvious if all numbers are equal to each other, that is x_i=x_j for any indices i and j.
Symbolically, it looks like
x_i=x_j ∀ i,j∈[1,n] ⇒ A_n = G_n


Solution B
(by Polya)

From the standard course of Math is known that the function y=e^x at point x=0 has a value y(0)=1 and has a tangential at 45°, which looks like this.

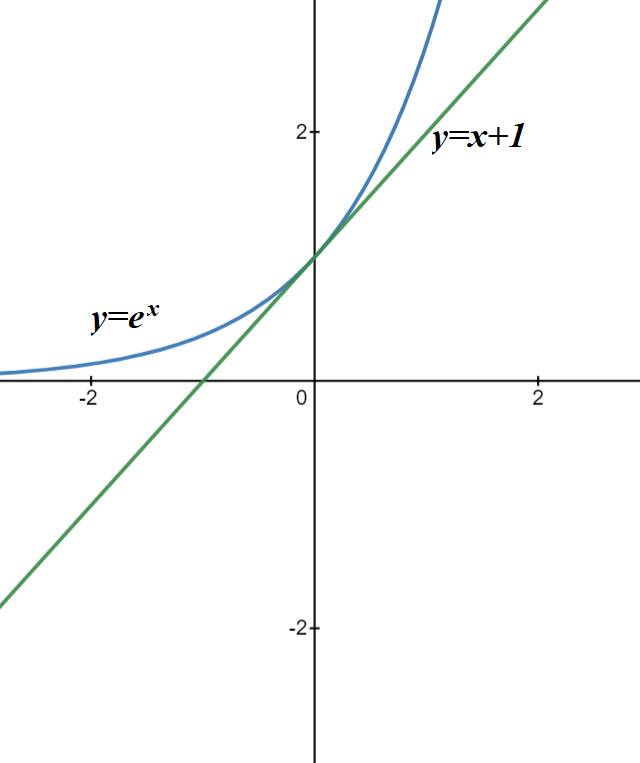
Shifting the graphs by 1 to the right by replacing x with x−1, we will have the following picture

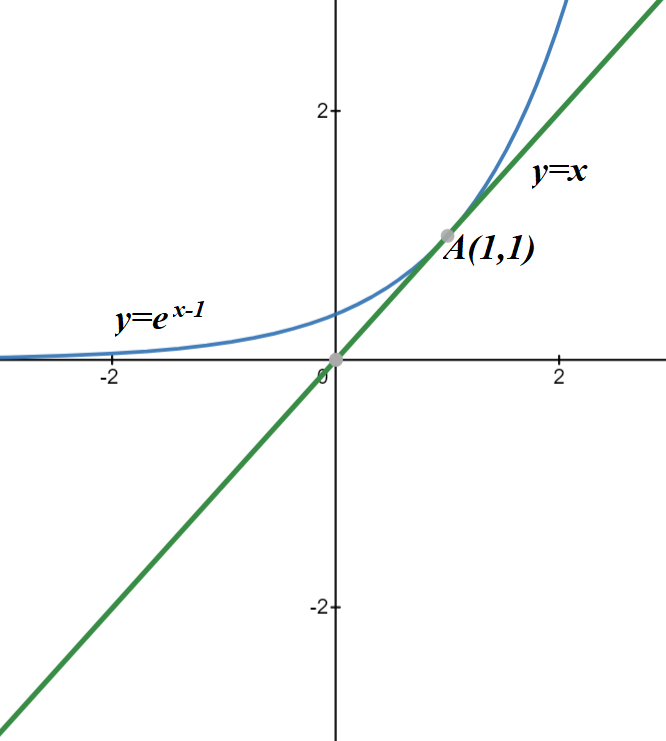
The last picture shows that the following inequality is held for all real values of x
e^x−1 ≥ x

Consider now a set of n non-negative numbers {x_i} (where i∈[1,n] and n is any natural number) with A being their arithmetic average and G being their geometric average (we are omitting a subscript n in averages for brevity).

Using an inequality above for x=x_i /A, we obtain
e^{(x_i /A)−1} ≥ x_i /A for any i or
A·e^{(x_i /A)−1} ≥ x_i

Multiplying the above inequality for all values of index i from 1 to n, we obtain
Aⁿ·e ^{Σ(x_i /A)−n} ≥ Π(x_i )

Interestingly, the exponent in the expression above is zero.
Here is why
Σ(x_i /A) = (1/A)·Σ(x_i) =
= (1/A)·A·n = n,
which makes the exponents in the inequality above equal to zero.

Therefore, considering e⁰=1, the inequality above looks like
Aⁿ ≥ Π(x_i )
A ≥ [Π(x_i )]^1/n = G
End of proof.