Geometry+ 04
This lecture is dedicated to planes, straight lines and their perpendicularity in three-dimensional space with Cartesian coordinates.
Problem A
Given a point P(a,b,c) in three-dimensional Cartesian space not coinciding with the origin of coordinates O(0,0,0).
What will be an equation for coordinates x, y and z that describes a plane going through origin of coordinates O(0,0,0) and is perpendicular to line OP?
Solution A
Let's use Vector Algebra techniques to solve this problem.
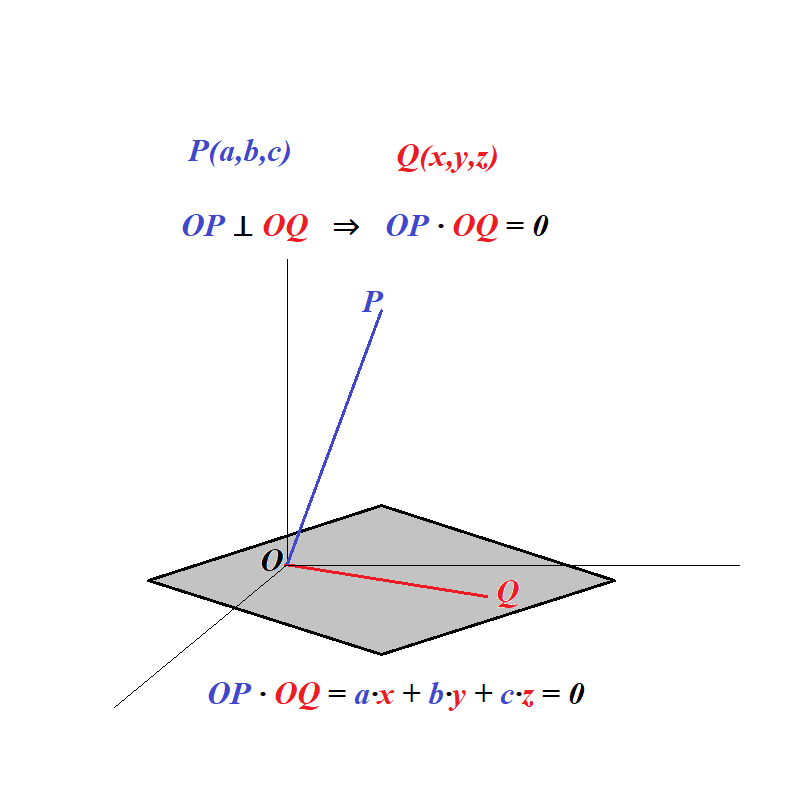
Consider a non-null vector OP originated at point O(0,0,0) with endpoint at P(a,b,c) and a plane that goes through point O(0,0,0) perpendicularly to vector OP at this point.
So, vector OP is normal to this plane.
Consider any point Q(x,y,z) on this plane and vector OQ.
This vector is lying completely within a plane because both its ends O and Q belong to this plane.
Therefore, since vector OP is, by assumption, perpendicular to the plane, it's perpendicular to vector OQ lying within this plane.
Two perpendicular vectors have their scalar product equal to zero.
Therefore, OP · OQ = 0
Let's express this in coordinates.
Vector OP in coordinate form is (a,b,c).
Since coordinates of point Q are (x,y,z), vector OQ in coordinate form is (x,y,z).
Now the scalar product of vectors OP and OQ is
OP · OQ =
= a·x + b·y + c·z
which is supposed to be equal to zero since these vectors are perpendicular.
Taking into account that there is one and only one plane perpendicular to a given vector OP at its origin O(0,0,0) and we have chosen any point Q(x,y,z) on this plane, the equation of a plane should be
a·x+b·y+c·z = 0
CONCLUSION 1
If vector (a,b,c) is normal to a plane going through the origin of coordinates (0,0,0) then the equation of this plane is
a·x+b·y+c·z = 0
CONCLUSION 2
The plane described by an equation
a·x+b·y+c·z = 0
is perpendicular to vector (a,b,c).
Problem B
Given a point P(a,b,c) in three-dimensional Cartesian space not coinciding with the origin of coordinates O(0,0,0).
What will be an equation for coordinates x, y and z that describes a plane going through point P and is perpendicular to a line connecting this point with the origin of coordinates O?
Solution B
Let's use Vector Algebra techniques to solve this problem.
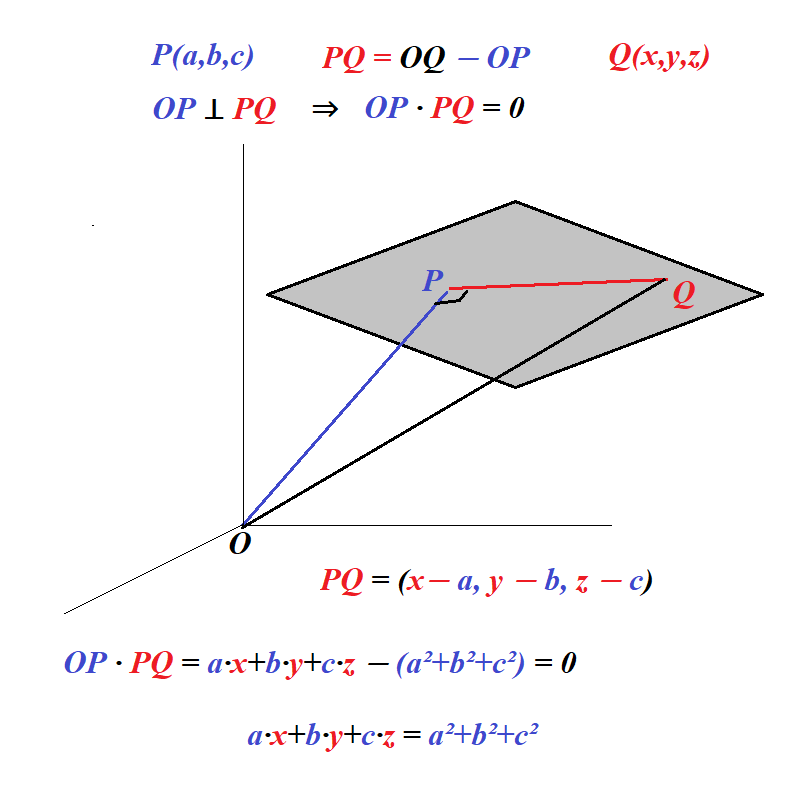
Consider a non-null vector OP originated at point O(0,0,0) with endpoint at P(a,b,c) and a plane that is assumed to be perpendicular to OP at point P.
So, vector OP is normal to this plane.
Consider any point Q(x,y,z) on this plane and vector PQ.
This vector is lying completely within a plane because both its ends P and Q belong to this plane.
Therefore, since vector OP is, by assumption, perpendicular to the plane, it's perpendicular to vector PQ lying within this plane.
Two perpendicular vectors have their scalar product equal to zero.
Therefore, OP · PQ = 0
Let's express this in coordinates.
Vector OP in coordinate form is (a,b,c).
Since coordinates of point Q are (x,y,z), vector OQ in coordinate form is (x,y,z).
Vector PQ can be represented as a difference between OQ and OP.
Therefore,
PQ = (x−a, y−b, z−c).
Now the scalar product of vectors OP and PQ is
OP · PQ =
= a·(x−a) + b·(y−b) + c·(z−c) =
= a·x+b·y+c·z − (a²+b²+c²)
which is supposed to be equal to zero since these vectors are perpendicular.
Taking into account that there is one and only one plane perpendicular to a given vector OP at its endpoint P(a,b,c) and we have chosen any point Q(x,y,z) on this plane, the equation of a plane should be
a·x+b·y+c·z − (a²+b²+c²) = 0
or
a·x+b·y+c·z = a²+b²+c²
CONCLUSION 1
If vector (a,b,c) is normal to a plane going through its endpoint (a,b,c) then the equation of this plane is
a·x+b·y+c·z = a²+b²+c²
CONCLUSION 2
The plane described by an equation
a·x+b·y+c·z = a²+b²+c²
is perpendicular to vector (a,b,c) at its endpoint (a,b,c).
Problem C
Given a plane α in three-dimensional Cartesian space going through the origin of coordinates O(0,0,0) and described by an equation
a·x + b·y + c·z = 0
What will be the coordinates p, q and r of an endpoint of a normal (perpendicular to plane α) vector originated at point O in terms of coefficients a,b,c defining the plane α?
Solution C
Obviously, point O(0,0,0) belongs to plane α because substituting x=0, y=0 and z=0 transforms the equation into an identity 0=0.
Let's choose any other point Q with coordinates (x,y,z) satisfying the equation of a plane α
a·x + b·y + c·z = 0
Consider vector OQ=(x,y,z).
Its origin is point O that belongs to our plane α.
Its endpoint Q(x,y,z) also belongs to this plane since plane α is a locus of all points satisfying the above equation.
Therefore, vector OQ lies within our plane α.
Assume, vector OP=(p,q,r) is normal to plane α at point O.
Its origin is the same point O as the origin of vector OQ=(x,y,z) that belongs to our plane.
Its endpoint P(p,q,r) lies somewhere in space.
Since OP ⊥ α, OP is perpendicular to any vector lying within plane α, including vector OQ.
Recall that necessary and sufficient condition for two vectors to be perpendicular to each other is their scalar product is zero.
OP · OQ = 0
Hence,
p·x + q·y + r·z = 0
The above equation is very much alike the equation of the plane
a·x + b·y + c·z = 0
Therefore, we should not look very far for values of p, q and r, but just choose p=a, q=b and r=c.
Now the equation of a plane α can be interpreted as a scalar product of two vectors OP=(a,b,c) and OQ=(x,y,z).
Since this scalar product is equal to zero, vectors OP and OQ are perpendicular to each other.
Since point Q(x,y,z) can be any point on a plane vector OP=(a,b,c) is perpendicular to the whole plane α defined by equation
a·x + b·y + c·z = 0
Answer C
The coordinates of an endpoint of a normal (perpendicular to plane α) vector originated at point O are (a,b,c).
Problem D
Given a plane α in three-dimensional Cartesian space described by a general equation
a·x + b·y + c·z + d = 0
Point O(0,0,0) is an origin of coordinates.
Assume, point P(p,q,r) belongs to plane α and vector
What will be the coordinates p, q and r of an endpoint of vector OP in terms of coefficients a,b,c,d defining the plane α?
Solution D
We have two conditions for coordinates p, q and r to satisfy:
1. Point P(p,q,r) belongs to plane α, which means
a·p + b·q + c·r + d = 0
2. Vector OP is normal (perpendicular) to plane α.
Consider any point Q(x,y,z) on plane α and vector PQ.
This vector is lying completely within a plane because both its ends P and Q belong to this plane.
Therefore, since vector OP is, by assumption, perpendicular to the plane, it's perpendicular to vector PQ lying within this plane.
Two perpendicular vectors have their scalar product equal to zero.
Therefore, OP · PQ = 0
Let's transform this into coordinates.
Vector PQ is a difference between OQ and OP.
Therefore, the coordinates of PQ are
(x−p, y−q, z−r)
Since OP ⊥ PQ, their scalar product is zero
p·(x−p)+q·(y−q)+r·(z−r) = 0
or
p·x+q·y+r·z−(p²+q²+r²) = 0
From the above equation we have to find p, q and r knowing that x, y and z satisfy the equation of a plane α
a·x + b·y + c·z + d = 0
Simple guess p=a, q=b and r=c is a good idea, but not a solution since
d ≠ −(p²+q²+r²)
To correct this situation, let's scale the vector (p,q,r)=(a,b,c) by some coefficient k to satisfy both conditions for a solution listed above.
First, let's find a scale factor k to make sure that endpoint P(k·a,k·b,k·c) of vector OP belongs to plane α.
Substituting x=k·a, y=k·b and z=k·c into equation that defines plane α, we obtain an equation for k:
a·k·a + b·k·b + c·k·c + d = 0
From this equation
k = −d/(a²+b²+c²)
This value of k is sufficient to put our point P(p,q,r) on the plane α.
Let's check that defined this way vectors OP and PQ are perpendicular to each other for any point Q(x,y,z) that satisfies the equation defining plane α
a·x + b·y + c·z + d = 0
Indeed,
OP · PQ =
= (k·a, k·b, k·c) ·
· (x−k·a, y−k·b, z−k·c) =
= k·(x·a + y·b + z·c) −
− k²·(a² + b² + c²)
where
a·x + b·y + c·z + d = 0 and
k = −d/(a²+b²+c²)
Substitute
a·x + b·y + c·z = −d and
(a²+b²+c²) = −d·k
getting
OP · PQ =
= k·(−d) −k²·(−d/k) = 0
So, since point Q(x,y,z) was chosen arbitrarily on plane α, vector OP is perpendicular to any vector on a plane and, therefore, to plane α itself.
Taking into account that P ∈ α, it proves that the coordinates p, q and r of an endpoint of vector OP are
p = −d·a/(a²+b²+c²)
q = −d·b/(a²+b²+c²)
r = −d·c/(a²+b²+c²)


No comments:
Post a Comment