Math+ Hyperbola Asymptotes: UNIZOR.COM - Math+ 4All - Geometry

Notes to a video lecture on http://www.unizor.com

Geometry+ Hyperbola Asymptotes

Let's start with a definition of an asymptote.
From less rigorous standpoint an asymptote to a curve is a straight line to which a curve goes infinitesimally close as a point of observation on our straight line moves to infinity.

More precisely, we assume that there is a plane with Cartesian coordinates on it.
There is some relationship between coordinates f(x,y)=0 that defines a curve on a coordinate plane that graphically represents it.
This relationship can be expressed as a function of one coordinate of another, like y=1/x or not in a functional way, like x·y=1.

In most cases we will consider the functional representation of dependency between coordinates, like y=f(x).

Vertical (parallel to Y-axis) asymptote to this function at point x=c where c, is a constant, is a line parallel to Y-axis and crossing X-axis at point x=c such that any one particular or any combination of the conditions below is true
lim_x→c f(x) = +∞ or = −∞
lim_x→c+0 f(x) = +∞ or = −∞
lim_x→c−0 f(x) = +∞ or = −∞
where x→c means that an argument x tends to value c in any possible way,
x→c+0 means that an argument x tends to value c while always being greater than c (tending from the right),
x→c−0 means that an argument x tends to value c while always being less than c (tending from the left).

The value of a function at exact point x=c might or might not be defined and is irrelevant.

Here is an example of a function with a vertical asymptote that satisfies the condition
lim_x→c f(x) = +∞
where f(x)=1/(x−2)² and c=2. 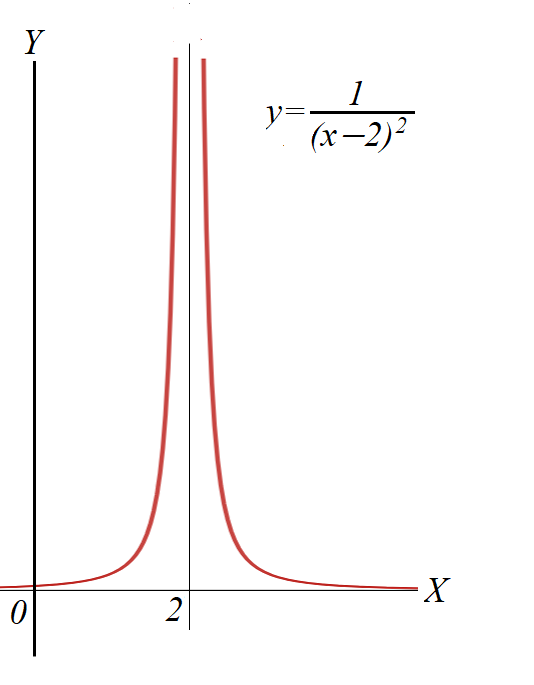Here is an example of a function with a vertical asymptote that satisfies the condition
lim_x→c+0 f(x) = −∞
where f(x)=ln(x−2) and c=2. 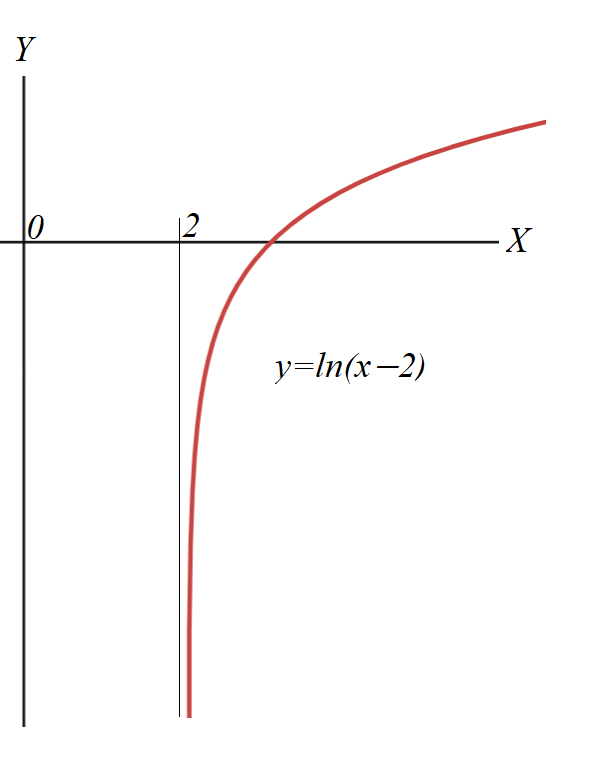Here is an example of a function with a vertical asymptote that satisfies the conditions
lim_x→c+0 f(x) = +∞
lim_x→c−0 f(x) = −∞
where f(x)=1/(x−2) and c=2.
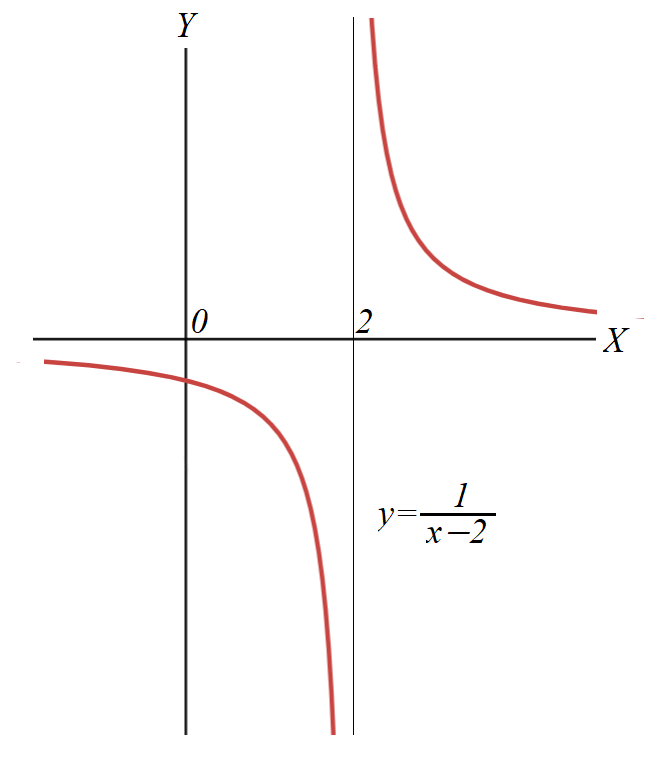
In any of the above cases the distance between a point on a vertical asymptote and a point on a curve in the direction perpendicular to an asymptote (that is, along a line parallel to X-axis) tends to zero as an argument tends to point c.

Horizontal (parallel to X-axis) asymptote has a different definition.
First of all, it's about a curve that represents a function getting infinitesimally close to a horizontal line as an argument tends to +∞ or −∞.
Obviously, we assume that this function is defined on an infinite segment.
Line y=c (c is a constant) is an asymptote for a function y=f(x) if
lim_x→+∞f(x) = c or
lim_x→−∞f(x) = c
Here is an example of a function with a horizontal asymptote that satisfies the condition
lim_x→−∞ f(x) = c
where f(x)=2+e^x and c=2. The distance between a point on a horizontal asymptote and a point on a curve in the direction perpendicular to an asymptote (that is, along a line parallel to Y-axis) tends to zero as an argument x tends to infinity.

Oblique (or slanted) asymptote for some function y=f(x) is a straight line L described by an equation y=a·x+b (a≠0) which is not parallel to any of the axes of a coordinate system, such that a distance from a point P[p,q]∈L (that is, q=a·p+b) to a point S[x,y] on a curve representing a graph of our function (that is, y=f(x)) in a direction perpendicular to line L (that is, PS⊥L) will be an infinitesimal variable, as a point P on a line L goes to infinity (that is if p→+∞ or p→−∞).

Here is an example of an oblique asymptote that satisfies a condition of infinitesimal closeness of a graph of a function to an asymptote as a value of an argument goes to infinity (positive or negative).

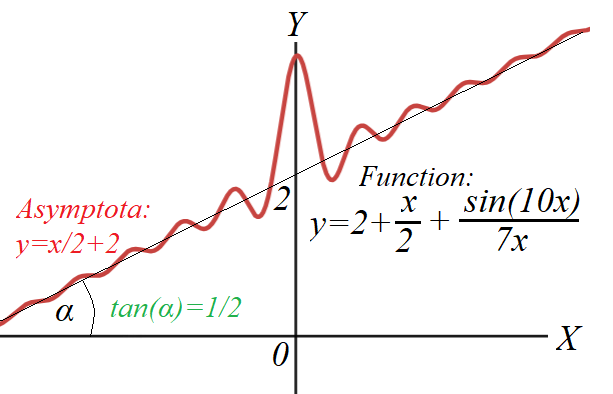
If a function is represented by a graph, and we expect that some straight line is an asymptote, the distance between any point on an asymptote and a graph of a function in a direction perpendicular to an asymptote must tend to zero as our point moves to infinity along an asymptote.
Let's derive the relationship between a function y=f(x) and its asymptote y=a·x+b.
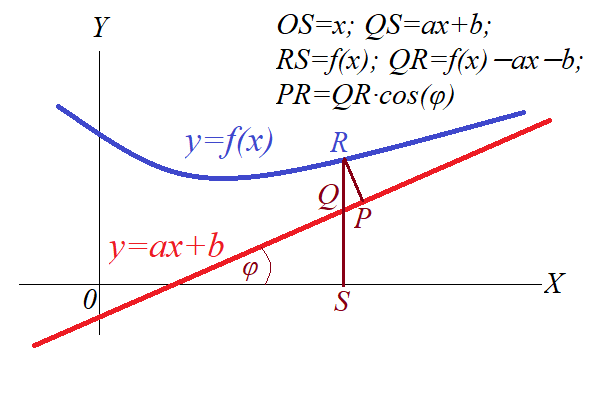Since PR=QR·cos(φ),
it will tend or not tend to zero exactly as QR=f(x)−a·x−b.
Therefore, if
lim_x→∞[f(x)−a·x−b]=0
then y=a·x+b is an asymptote.

Let's use this result to find asymptotes of a hyperbola defined by an equation
x²/a² − y²/b² = 1
Let's concentrate on the top right branch of this hyperbola, that we can express as function
y = √x²·b²/a² − b²

Without subtracting a constant b² under a square root, the equation above would look like y=(b/a)·x - straight line.
This prompts us that a straight line y=(b/a)·x might be an asymptote.
Let's check it out.

lim_x→∞[√x²·b²/a²−b²−(b/a)·x]=
multiply and divide by √x²·b²/a²−b²+(b/a)·x
= 0
because we will have a constant −b² in the numerator and a function in the denominator that monotonically tends to infinity.

Analogously, a line y=−(b/a)·x is an asymptote to the top left side of a graph.