Math+ Parabola Optics: UNIZOR.COM - Math+ 4 All - Geometry

Notes to a video lecture on http://www.unizor.com

Geometry+ Parabola Optics

Though the word "optics" sounds very much like a topic of Physics, we will consider strictly mathematical aspect of it.
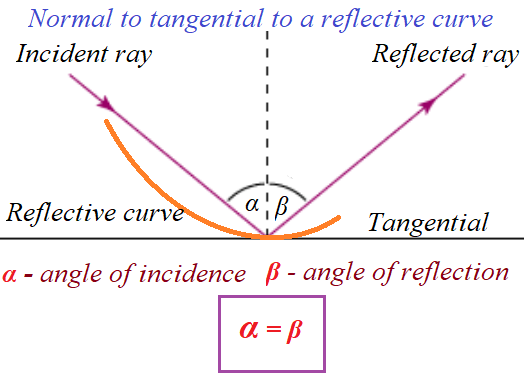
One of the properties of parabola is that if its contour is reflective, a ray of light emitted from its focus will be reflected parallel to its axis of symmetry regardless of the direction it was sent.

Reflection of a curve occurs exactly as if, instead of a curve at the point of incidence, there was a tangential line to a curve, and reflection was of that tangential straight line.

Consider a parabola with focus F(c,0), directrix d, point P(x,y) on this parabola and tangential BC to a parabola at point P(x,y).
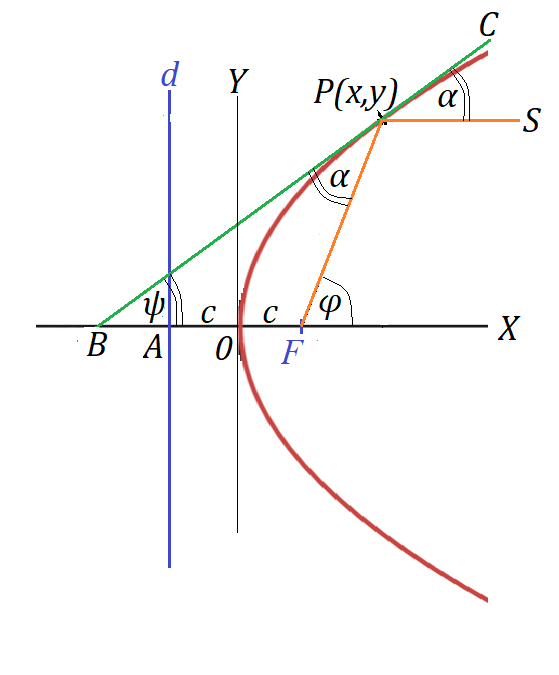The ray of light is emitted from a focus F(c,0), goes to point P(x,y) and reflects along PS.
Because of the laws of reflection, angles ∠FPB and ∠SPC are equal, they are marked as α.
If we prove that these angles α are also equal to angle ∠ψ the tangential at point P line BC makes with the axis of symmetry of parabola BX, it will prove the parallelism of reflected ray PS with line BC, regardless of position of point P on a parabola.

Our plan to prove it is to prove that tan(α)=tan(ψ), from which the equality α=ψ follows because function tan() is monotonic for these angles.

Since sum of angles of a triangle ΔBPF equals to π,
α + ψ + (π−φ) = π
Therefore,
α = φ − ψ
We can calculate tan(α) using a formula for tangent of difference between angles, we can express tan(α) in terms of tan(φ) and tan(ψ).
tan(α) =
= [tan(φ)−tan(ψ)]/[1+tan(φ)·tan(ψ)]

Angle ∠φ=∠XFP.
Knowing coordinates of points P(x,y) and F(c,0), it's easy to calculate
tan(φ) = y/(x−c)

As we know, a tangent of an angle between a tangential line to function f(x) at some point and X-axis is a function's derivative f'(x) at that point.
Therefore, tan(ψ)=y'(x)
Since an equation of a parabola is y²=4c·x, differentiating this equation we get
2y·y' = 4c
Hence, y' = 2c/y = tan(ψ).

Now we have all the components to calculate tan(α):
tan(α) =
= [y/(x−c)−2c/y]/[1+(y/(x−c))·(2c/y)]
Let's simplify this expression.
Its numerator equals to
(y²−2c·x+2c²)/(x·y−c·y)
But for each point of a parabola y²=4c·x.
Use it in the formula above, getting the same numerator as
(4c·x−2c·x+2c²)/(x·y−c·y) =
= 2c·(x+c)/(x·y−c·y)
The denominator in the formula above can be simplified as
1 + (y/(x−c))·(2c/y) =
= 1 + 2c·y/((x−c)·y) =
= (x·y−c·y+2c·y)/((x−c)·y) =
= y·(x+c)/(x·y−c·y)

Dividing the numerator
2c·(x+c)/(x·y−c·y)
by denominator
y·(x+c)/(x·y−c·y)
we get the value of tan(α) as
tan(α) = 2c/y

But this is the same value as tan(ψ), which proves that angles ∠α and ∠ψ are equal, which, in turn, proves that lines PS (reflected ray of light) and FX (axis of symmetry of a parabola) are parallel regardless of the position of point P on a parabola.

Therefore, all the rays from the parabola's focus directed in any direction will be reflected in one direction - parallel to the axis of symmetry of this parabola.