Unizor - Definite Integrals - Length of Curve

Notes to a video lecture on http://www.unizor.com

Definite Integrals -
Length of Curve

Our task is to calculate a length of a curve on a coordinate plane, defined parametrically as a set of points (x(t),y(t)), where x(t) and y(t) are smooth functions of parameter t∈[a,b].

This is one of the typical integration problem and can be approached similarly to our approach to calculate the area under a curve.

Let's break down a segment [a,b] into N intervals by points a=t₀, t₁,...t_N=b, which results in corresponding breaking of our curve into smaller pieces by points
(x₀,y₀)=(x(t₀),y(t₀)),
(x₁,y₁)=(x(t₁),y(t₁)),...
...
(x_N,y_N)=(x(t_N),y(t_N)),

Each small piece of a curve can be approximated with a straight line from one of its ends to another, and this approximation will be better with the density of break points increasing.
So, the n-th piece of a curve is approximated with a segment from point (x_n−1,y_n−1) to point (x_n,y_n).

The length of this n-th piece of a curve L_n can be calculated using the regular formula of a length of a segment between two points on a plane:
L_n² = (x_n−x_n−1)²+(y_n−y_n−1)²

Taking into account that both coordinates are functions of parameter t, we can express it differently:
L_n² = (x(t_n)−x(t_n−1))² +
+ (y(t_n)−y(t_n−1))²

Notice that
x(t_n)−x(t_n−1) ≅ x^I(t_n)·(t_n−t_n−1)
where x^I(t) is a derivative of function x(t) by t and approximation gets better and better as we increase the density of points t_n.

So, we can express the length of the n-th piece of a curve as
L_n² ≅ [x^I(t_n)² + y^I(t_n)²] ·
· (t_n−t_n−1)²

From this we get
L_n ≅ SQRT[x^I(t_n)² + y^I(t_n)²] ·
· (t_n−t_n−1)

As before, we use Δt_n=t_n−t_n−1.
Now the length of a curve can be approximated by this sum:
L ≅ Σ_n∈[1,N] L_n ≅
≅ Σ_n∈[1,N] f(x_n)·Δt_n
where
f(t)=SQRT[x^I(t)² + y^I(t)²]

Recall the definition of the definite integral:
∫_a^bf(x) dx =
= lim Σ_i∈[1,N] f(x_i)·Δx_i
where Δx_i=x_i−x_i−1 represents partitioning of segment [a,b] into N parts, and it is assumed that the widest interval Δx_i is shrinking to zero by length as N→∞.

Clearly, we are dealing with an integral in our case. The sum of pieces of our curve represents Riemann sum, and the limit of this sum, as the density of points t_n increases, is the following integral:
∫_a^bSQRT[x^I(t)² + y^I(t)²] dt

So, the length of the curve on a coordinate plane, defined parametrically by coordinate functions x(t) and y(t), where t∈[a,b], equals to
∫_a^bSQRT[x^I(t)² + y^I(t)²] dt

Let's apply this to a couple of practical problems.

Problem 1
Calculate the length of a circle of radius R.

Solution
To define a circle parametrically, let's choose an angle between its radius and a positive direction of the X-axis as a parameter t∈[0,2π].
Then the X-coordinate of a point on a circle, whose radius forms an angle t with positive direction of the X-axis, equals to x(t)=R·cos(t) and Y-coordinate equals to y(t)=R·sin(t).

Now we can use the above formula to calculate the length of circle.
∫₀^2πSQRT[x^I(t)² + y^I(t)²] dt =
= ∫₀^2πSQRT[R²sin²(t) +
+ R²cos²(t)] dt =
= ∫₀^2πR dt =
= R·2π − R·0 = 2πR
As we see, the length, as we counted, equals to the one in a classical formula for the length of the circle. No surprise here.
The end.

Problem 2
Calculate the length of an astroid given parametrically as
x=R·cos³(t), y=R·sin³(t)
where t∈[0,2π]

Solution
Astroid looks like this:

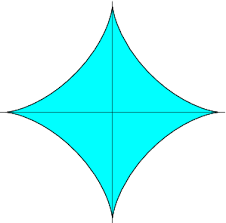
Its vertices are at distance R from the origin, and its four arcs correspond to parameter t changing in each quadrant from 0 to 2π.
Using the symmetry, lets' calculate the length of only one arc for t∈[0,π/2] and then multiply it by four.
First, calculate the derivatives by t:
x^I(t) = −3R·cos²(t)·sin(t)
y^I(t) = 3R·sin²(t)·cos(t)
Now we use the formula for the length of a curve.
SQRT[x^I(t)² + y^I(t)²] =
= 3R·|sin(t)·cos(t)| =
= (3/2)R·|sin(2t)|
This should be integrated within margins t∈[0,π/2].
Within these margins 2t changes from 0 to π and sin(t) is non-negative, so we can drop absolute value.
So, we need to find the following integral:
∫₀^π/2(3/2)R·sin(2t) dt
Indefinite integral of sin(2t) is −cos(2t)/2, which means that we have to calculate the following
(−cos(π)/2) − (−cos(0)/2) =
= 1/2 + 1/2 = 1.
Therefore, the length of one quarter of an astroid equals to (3/2)R·1 = (3/2)R and the length of an entire astroid is (3/2)R·4=6R.
The end.