Unizor - Partial Differential Equations - Heat Equation

Notes to a video lecture on http://www.unizor.com

Partial Differential Equations
Overview - Heat Equation

Since we talked about ordinary differential equations, where a function of one argument together with its derivatives participates in the equation, we might as well touch on differential equations, where function of two (or more) arguments together with its partial derivatives participates in the equation. These equations are called partial differential equations.

In order to present this material in a more practical light and to emphasize the importance of differential equations (particularly, partial) in practical applications, let's discuss one particular physical process that naturally leads to partial differential equations.

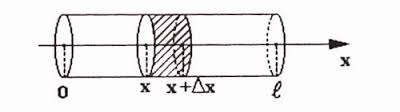
Let's imagine an insulated thin metal rod heated on one end and examine how its temperature T at different distance from the edge changes with time.
We assume that the rod is stretched along the X-axis with its heated end at origin. The distance from this end to any point on a rod is X-coordinate of this point. Time t will be measured from the moment the heat is applied to the edge at x=0.

Considering our rod is insulated and thin, we can safely assume that the heat dissipates only along its length from point x=0 towards the other edge, and the rod's temperature is a function of two arguments:
distance x from the edge
and time t:
T = T(t,x)
The illustration below will be handy in our analysis.


Before embarking on calculations let us remind a few physical properties that affect the process of heat dissipation.

1. Heat Q - a form of energy manifested in vibration of molecules of an object.
It is measured in the same units as energy.

2. Temperature T - a measure of intensity of the molecular vibration.
It is measured in degrees of different scales.

3. Specific heat capacity C - an amount of energy (heat) needed to increase temperature of a unit of mass by a unit of temperature.
It is assumed to be a constant for any specific material within reasonable range of temperatures and precision.
If an object of mass m increased in temperature by ΔT, it consumed ΔQ=C·m·ΔT units of heat (energy).

4. Thermal conductivity k - a measure of how fast molecular vibration is transferred within an object.
It was experimentally established that the amount of heat transferred from one zone of an object to another per unit of time through a unit of area on the boundary between these zones is proportional to a rate of change of temperature at this boundary and depends on the qualities of the material. For every material it is a constant within a reasonable range of temperatures.
In one-dimensional case on an above picture of a thin rod that has area S of crosscut, when the heat is transformed through a point x and the rate of change of temperature at that point and at that time is ∂T(t,x)/∂x, the amount of heat that goes through during time Δt can be calculated as
ΔQ = −k·S·Δt·∂T(t,x)/∂x
Minus in this equality reflects that heat is transferred from hot to cold area and, therefore, the partial derivative of temperature T by x is negative, while energy must be positive.

Now we are ready to connect all the parameters mentioned above into one heat equation.

Consider a part of a thin rod from point x to point x+Δx.
As the heat dissipates from left to right, during the time Δt certain amount of heat enters this area through crossing at point x and certain amount of heat exits this area through crossing at point x+Δx.

The heat entering through crossing at point x measures
ΔQ_in = −k·S·Δt·∂T(t,x)/∂x
The heat exiting through crossing at point x+Δx measures
ΔQ_out = −k·S·Δt·∂T(t,x+Δx)/∂x

The difference between them is an amount of heat that contributed to a rise in temperature of the part of a rod from x to x+Δx. This difference equals to
(A) ΔQ₊ = k·S·Δt·[∂T(t,x+Δx)/∂x − ∂T(t,x)/∂x]

On the other hand, the heat ΔQ₊, consumed by a part of a rod of length Δx, area of crosscut S and specific heat capacity C should increase the temperature by ΔT related to this heat as
ΔQ₊ = C·m·ΔT
where m is a mass of this part of a rod, that can be calculated as
m = ρ·S·Δx
where ρ is a mass of a unit of volume of the material this rod is made of.
Therefore,
(B) ΔQ₊ = C·ρ·S·Δx·ΔT

From equations (A) and (B) we derive the following equality:
C·ρ·S·Δx·ΔT = k·S·Δt·[∂T(t,x+Δx)/∂x − ∂T(t,x)/∂x]
This can be transformed into
ΔT/Δt = [k/(C·ρ)]·[∂T(t,x+Δx)/∂x−∂T(t,x)/∂x]/Δx

When Δt→0 and Δx→0 our equation can be represented as
∂T(t,x)/∂t = [k/(C·ρ)]·∂²T(t,x)/∂x²

Traditionally, this heat equation is written as
∂T(t,x)/∂t = a²·∂²T(t,x)/∂x²
where a² = k/(C·ρ)