Unizor - Partial Derivatives - Stationary Points

Notes to a video lecture on http://www.unizor.com

Partial Derivatives Properties - Stationary Points

We will mostly be concerned with partial derivatives of functions with two arguments.
The theory can be extended to functions of any number of arguments, but it's outside of the scope of this course.
Besides, functions of two arguments can be visualized as surfaces in three-dimensional space to better understand their properties.

Stationary points are those, where both partial derivatives of function f(x,y) of two arguments are equal to zero.

Let
g(x,y)=∂f(x,y)/∂x
h(x,y)=∂f(x,y)/∂y

Definition:
Point (a,b) is a stationary point for function f(x,y) if g(a,b)=0 and h(a,b)=0.

Theorem
A smooth function f(x,y) of two variables that has a local maximum at point (a,b) has both of its partial derivatives at this point equal to zero.

Proof

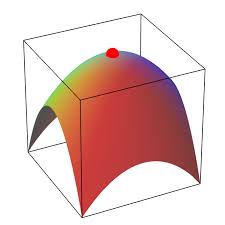
Let's prove that ∂f(x,y)/∂x=0 for x=a and y=b. The proof for other partial derivative ∂f(x,y)/∂y is analogous.
So, we fix variable y=b and calculate the partial derivative of f(x,y) by x at point x=a as follows:
∂f(x,y)/∂x = {at x=a,y=b} = lim[f(a+Δx,b)−f(a,b)]/Δx
(the limit is taken as Δx→0)
Since point (a,b) is a local maximum, the numerator [f(a+Δx,b)−f(a,b)] is negative, while the denominator Δx=(x+Δx)−x is non-positive for x+Δx ≤ x and non-negative for x+Δx ≥ x.
For a sufficiently smooth function (at least, we need the continuity of partial derivatives) this implies that the limit above must be equal to zero.

So, we have proven that for a smooth function of two variables the necessary condition for having a local maximum at point (a,b) is the equality of its partial derivatives to zero at this point.

The situation with local minimum is analogous and the equality of partial derivatives to zero at some point is a necessary condition for having a local minimum at this point.


IMPORTANT NOTE
The equality of partial derivatives to zero at some point is only a necessary condition for a function to have a local maximum or minimum at that point. It's not a sufficient condition.
This is similar to a situation with functions of one variable, when a derivative can be zero at some point, but a function can have an inflection point like function y=x³ at point x=0.
For a function of two variables a situation like this might occur when it has a saddle point.
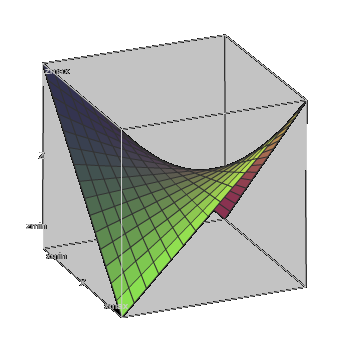
Here is an example:

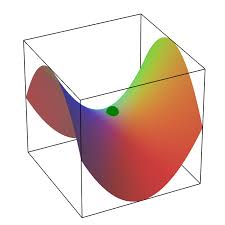
At the point in the middle of this "saddle" both partial derivatives are equal to zero, but this point is not a local minimum or maximum of a function.

Obviously, we would like to differentiate cases of a stationary point being a local maximum, a local minimum or a saddle point similarly to a situation with functions of one argument, where the second derivative sign (positive or negative) indicated whether a stationary point is minimum, maximum or inflection point.

Here is the rule, which we provide without rigorous proof.
Let's assume that function f(x,y) can be partially differentiated twice (that is, ∂f(x,y)/∂x, ∂f(x,y)/∂y, ∂²f(x,y)/∂x², ∂²f(x,y)/∂y², ∂²f(x,y)/∂x∂y exist) and all second partial derivatives are continuous.
Let's further assume that at point (a,b) both first partial derivatives equal to zero:
∂f(x,y)/∂x = 0 at x=a, y=b
∂f(x,y)/∂y = 0 at x=a, y=b
Consider the expression
Δ = ∂²f(x,y)/∂x² · ∂²f(x,y)/∂y² − [∂²f(x,y)/∂x∂y]²
at point x=a, y=b.
The rule is:
if Δ < 0, (a,b) is a saddle point;
if Δ > 0, (a,b) is a local minimum or local maximum point and the sign of ∂²f(x,y)/∂x² or ∂²f(x,y)/∂y² can be used to distinguish minimum from maximum (positive for minimum, negative for maximum and these two second derivatives must have the same sign since otherwise Δ would be negative).
All other cases are not sufficient to determine the behavior of the function at this point.

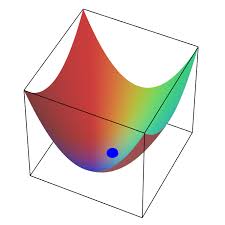
Example 1

f(x,y)=1/(1+x²+y²)

∂f(x,y)/∂x = −2x/(1+x²+y²)²
∂f(x,y)/∂y = −2y/(1+x²+y²)²
At point (0,0) both partial derivatives are equal to zero, therefore (0,0) is a stationary point.
Examine the second derivatives.
∂²f(x,y)/∂x² = (6x²−2y²−2)/(1+x²+y²)³
∂²f(x,y)/∂y² = (6y²−2x²−2)/(1+x²+y²)³
∂²f(x,y)/∂x∂y = 8x·y/(1+x²+y²)³
At point x=0, y=0 the three expressions above can be used to calculate
Δ = (−2)·(−2)−0² = 4
Since Δ is positive, we have a local minimum or maximum at point (0,0). To distinguish between them, look at the sign of the second partial derivative by x. It is negative. Therefore, we have a local maximum as is obvious from the graph above.

Example 2

f(x,y)=x·y

∂f(x,y)/∂x = y
∂f(x,y)/∂y = x
At point (0,0) both partial derivatives are equal to zero, therefore (0,0) is a stationary point.
Examine the second derivatives.
∂²f(x,y)/∂x² = 0
∂²f(x,y)/∂y² = 0
∂²f(x,y)/∂x∂y = 1
At point x=0, y=0 the three expressions above can be used to calculate
Δ = 0·0−1² = −1
Since Δ is negative, we have a local saddle point (0,0), as is obvious from the graph above.