Electromagnetic Field Equations 1
This and a few subsequent lectures are about certain laws related to properties of electromagnetic field expressed in a format of equations.
These laws, in their general mathematical form, were formulated in 19th century by a Scottish mathematician and scientist James Maxwell. We will concentrate on their meaning and mathematical expression in some simple cases.
We assume that the concepts of electric and magnetic fields are known by now from the "Electromagnetism" part of this course.
One of the concepts introduced there was the electric field intensity E - a vector defined at each point of space where electric field exists, that is a vector field, acting as a force on any electric charge proportional to its amount of charge.
In particular, if the electric field is produced by a point charge q0 located at point O, all vectors of electric field intensity are radial, directed towards or away from point O depending on its charge (positive or negative). Then on the distance r from O at point P the magnitude of the electric field intensity equals to E=k·q0 /r², it's directed from O to P for positive charge q0 or from P to O for negative q0.
In this formula the constant k is often expressed as k=1/(4πε), where ε is the permittivity of the media between points O and P with ε0 used for permittivity of vacuum and εr=ε/ε0 defined as relative permittivity of the media.
In general, an electric field intensity E (a vector) produces a force Fe (also a vector) on any charge q:
Fe = q·E
The Gauss Law - Electric
At any point of the electric field, where its intensity vector E is defined, we can position an infinitesimal flat piece of surface σ and calculate the electric field flux ΦE(σ) flowing through it.
This flux is defined as a scalar product of two vectors - the vector of electric field intensity E and a normal vector A to a piece of a surface σ proportional in its magnitude to an area of this piece of surface and directed perpendicularly to it:
ΦE(σ) = E·A
where |A| = area(σ) and A⊥σ.
The picture below illustrates this:
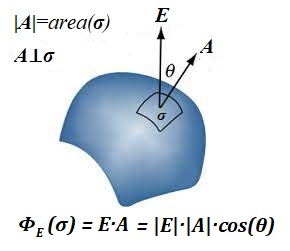
If electric field intensity vector is already perpendicular to a piece of a surface, the flux is just a product of magnitude of this vector and an area of a piece of a surface.
Consider a simple case of a point charge q. Space around it constitutes the electric field and, as mentioned above, the vector of electric field intensity E is radial and its magnitude on a distance r equals to E=k·q/r² where constant k=1/(4πε).
Consider a sphere of radius r with a center at this point charge. Since the magnitude of a vector of electric field intensity is constant on this sphere and the direction of this vector is always radial (which implies that it's perpendicular to a sphere's surface), the total electric field flux through a sphere can be expressed as a product of the magnitude of the electric field intensity by an area of a sphere:
ΦE=[1/(4πε)]·(q/r²)·4πr²=q/ε
We have received a wonderfully simple formula that states that the total flux of electric field through a sphere does not depend on a radius of this sphere, it depends only on amount of charge inside this sphere and the permittivity of a media.
Remarkably, the same result we would be able to obtain, if the surface around a point charge is not exactly spherical, but is any closed surface.
The mathematics of it are a little more involved, and we just state this as a fact.
Moreover, the charge inside a closed surface does not have to be a point charge. Any distribution of charge inside a closed surface will produce the same result - the total flux through a surface is the total amount of charge divided by permittivity of media. It's easy to understand because multiple fields have a property of superposition - total intensity is a vector sum of individual component intensities.
The above is the Gauss Law for electric field.
As a trivial consequence, imagine any closed surface, like a cube or ellipsoid, in the electric field with no charge inside it.
According to Gauss Law, the flux of electric field through this closed surface must be zero, which is understandable because what comes in should get out without any addition or subtraction since there is no charge inside.
On the other hand, if there is a charge inside this surface, it will contribute its electric field intensity to the one that came from outside, which will distort the balance between incoming and outgoing electric field intensities. It the charge outside was positive and the one inside was positive as well, the resulting outgoing from a surface intensity will be greater than incoming. Same with negative outside and negative inside.
A different form of the same law can be obtained by making the following thought experiment.
Assume we have electric field in three-dimensional Cartesian coordinate space of intensity E(x,y,z) at point {x,y,z} produced by electric charge distributed in space with density ρ(x,y,z).
Let's consider a very small (of course, we intend to shrink it to infinitesimal) parallelepiped aligned along coordinate planes with one corner at point A{x,y,z} and dimensions Δx⨯Δy⨯Δz.
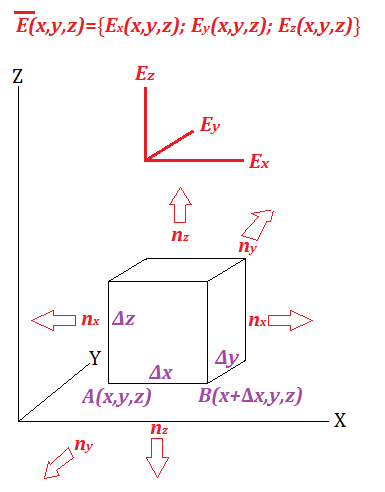
Inside this parallelepiped there is some charge, which we can consider to be uniform since our parallelepiped is very small:
q=ρ(x,y,z)·Δx·Δy·Δz
This charge will emit electric field to all six sides of a parallelepiped.
Our plan is to calculate the total flux of the electric field through a surface of this parallelepiped and equate it to a total charge inside, which, according to the Gauss Law discussed above, should be equal to this flux (with a factor ε).
Let's consider X-, Y- and Z-components Ex(x,y,z), Ey(x,y,z) and Ez(x,y,z) of a vector of field intensity E(x,y,z).
Let's calculate the flux through the right side of a parallelepiped and its left side, separated by Δx.
We have to consider only Ex component of the electric field intensity vector since other components are parallel to surfaces under consideration.
The flux on the right side is
Φright = Ex(x+Δx,y,z)·Δy·Δz
The flux on the left side is
Φleft = −Ex(x,y,z)·Δy·Δz
(minus sign in front is used because the direction of a normal vector on the left side of the parallelepiped is opposite to the one on the right side)
Sum of both is the flux going through parallelepiped in the X-direction of the space:
Φx = [Ex(x+Δx,y,z)−Ex(x,y,z)]·
·Δy·Δz
Considering we intend to make all Δ dimensions infinitesimal, the difference between two values of Ex can be expressed as
Ex(x+Δx,y,z)−Ex(x,y,z) =
= [∂Ex(x,y,z)/∂x]·Δx
Now the flux along the X-axis is
Φx = [∂Ex(x,y,z)/∂x]·Δx·Δy·Δz
Analogously, flux along the Y-axis is
Φy = [∂Ey(x,y,z)/∂y]·Δx·Δy·Δz
And along Z-axis:
Φz = [∂Ez(x,y,z)/∂z]·Δx·Δy·Δz
The total electric field flux through and the total charge inside a parallelepiped, according to the Gauss Law are related as
Φx + Φy + Φz = q/ε
As we noted above, the total charge inside a parallelepiped is
q=ρ(x,y,z)·Δx·Δy·Δz
Therefore,
∂Ex(x,y,z)/∂x +
+ ∂Ey(x,y,z)/∂y +
+ ∂Ez(x,y,z)/∂z = ρ/ε
To simplify a notation, mathematicians came up with a construction that looks like a vector with three components:
∇ = {∂/∂x, ∂/∂x, ∂/∂x}
Then a construction that resembles a scalar (dot) product of this pseudo-vector ∇ and a real vector
∇·E=∂Ex/∂x+∂Ey/∂y+∂Ez/∂z
With all these assumptions the Gauss Law in this differential form looks really short and simple:
∇·E = ρ/ε
The above equation is the first of four Maxwell differential equations that describe the electromagnetic field.


No comments:
Post a Comment