Circulation of Vector Field
Consider a two-dimensional vector field F(x,y) with components
{Fx(x,y),Fy(x,y)}
For definitiveness, assume that vectors F(x,y) represent some force that can act on objects positioned at any point {x,y} on the coordinate XY-plane. For example, our plane is a surface of water and the wind blows on paper ships on it. So, at any given moment of time the vectors at any point of this two-dimensional vector field are defined by the magnitude and direction of the wind at that point, as represented by arrows on a picture below.
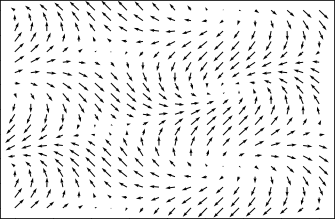
Consider now that the wind does not change and our task is to move a paper ship along some trajectory from point A to point B.
How much work should we perform?
We will consider different cases, increasing the complexity.
Uniform Vector Field and Straight Path
So, our field F(x,y) consists of vectors equal to each other and equal to the same vector F for all points {x,y} on a plane, and our path AB is a straight line.
This is a simple problem from Mechanics.
First, we have to find a projection FAB of vector F onto line AB and then multiply the magnitude of this projection by the length from A to B:
W = |FAB|·|AB|
Using scalar (dot) product of vectors, the same can be expressed as
W = (F·AB)
where AB is a vector from A to B.
If vector F is perpendicular to AB, the scalar product is zero and the work is zero, since the wind does not prevent us to move the ships from A to B nor helps us.
If vector F is collinear with AB, the scalar product is a product of a magnitude of F and a length of AB, taken with a positive sign if the direction of vector F is from B to A and we actually perform work against the wind or taken with a negative sign if the direction of vector F is from A to B and it's the field instead, not we, moves the ship.
If our segment AB is positioned along the X-axis and vector F has components {Fx,Fy}, the work is a product of Fx by a length of AB, taken with appropriate sign, as above.
Non-uniform Vector Field and Straight Path
Assume again that points A and B are on the X-axis.
Now vectors F(x,y) are not the same, their magnitude and directions are functions of point {x,y}.
Since F(x,y)=Fx(x,y)+Fy(x,y), the work against vector F(x,y) can be expressed as a sum of work against its component Fx(x,y), that is collinear with our path AB, and work against its component Fy(x,y), that is perpendicular to our path AB.
Obviously, the latter is zero since Fy(x,y) is perpendicular to path AB.
To calculate the work against Fx(x,y) along path AB (that is, for x from x=A to x=B, while y=0), we break segment AB into many tiny intervals of the same length Δx by points
x0=A, x1, x2,...,xn=B
Assuming that each interval is small enough, so Fx(x,0) does not significantly change within it, the work, approximately, equals to
W = Σi∈[1,n]Fx(xi,0)·Δx
All we need now to have exact value for work is to go to a limit with Δx→0 (assuming, the limit exists), getting
W = ∫[A,B]Fx(x,0)·dx
Non-uniform Vector Field and Curved Path
Our task is to move a paper ship from point P(xp,yp) to point Q(xq,yq) along a defined curved path in the two-dimensional vector force field F(x,y) and calculate the work performed on the way.
This case leads us to integration along a curved path.
This process is not much different from regular definite integral of some function f(x) on a segment x∈[a,b].
First, we break a curved path from point P(xp,yp) to point Q(xq,yq) into many tiny pieces, so small that each one is practically straight and vector field F(x,y) within each piece can be considered constant.
Now our problem to find a total work needed to move a paper ship against the wind from P to Q can be expressed approximately as a sum of works on each almost straight tiny segment against almost constant vector force field.
As we break the path into smaller and smaller pieces, our calculation will be more and more precise, and in the limit case we will come up with exact value of work performed.
The calculation of work on each straight path with constant vector field along it was described above in the part Uniform Vector Field and Straight Path.
All we need is to construct a scalar (dot) product of the vector of force F(x,y), considered constant in the tiny interval around each point {xi,yi}, by the length of ith interval, considered as a vector from {xi-1,yi-1} to {xi,yi}. Then we will sum up all the results from all pieces of a path.
To accomplish this, assume that we actually move along a curved path from P to Q in real time t. At t=0 we are at point P and at time t=T we arrive at point Q.
Our journey along the path on a two-dimensional plane can be described as a function of time: {x(t),y(t)}.
Let's break the total time from 0 to T into many tiny intervals, each equal to Δt:
{t0=0, t1, t2,...tn=T}
Our position along a path at time ti will be {x(ti),y(ti)} with {x(t0),y(t0)}=P and {x(tn),y(tn)}=Q.
Let the velocity of our movement along a path be
V(x,y) = {dx(t)/dt, dy(t)/dt}
This vector is always tangential to a path of motion, that is directed along each tiny piece of a curved path.
The length of the ith piece of a path equals to |V(xi,yi)|·Δt.
Therefore, the work performed on the ith piece of a path equals
ΔWi = (F(xi,yi)·V(xi,yi))·Δt
(here the first multiplication is a scalar product of two vectors, the second one is a product of two scalars)
Now we are ready to calculate approximate work performed on the whole path:
W[PQ] ≅ Σi∈[0,n]ΔWi =
= Σi∈[0,n](F(xi,yi)·V(xi,yi))·Δt
Familiarity with a definition of the definite integral would lead to expression for the limit of approximate work above to its exact value
W[PQ] =
= ∫(F(x(t),y(t))·V(x(t),y(t)))·dt
where integration is performed in the time interval t∈[0,T]
As you see, an integration along a curved path is reduced to familiar process of integration on a time interval [0,T], as long as we know how we move along a path:
position r(t)={x(t),y(t)} and
velocity, which is a derivative of a position by time
V(x(t),y(t)) = dr(t)/dt =
= {dx(t)/dt,dy(t)/dt}.
Using a position vector r(t)={x(t),y(t)}, the formula about total work performed on the path from P to Q can be written as W[PQ] =
=∫[0,T](F(x(t),y(t))·dr(t)/dt)·dt=
= ∫[0,T](F(x(t),y(t))·dr(t))
or, simpler,
W[PQ] = ∫[PQ](F·dr),
assuming the integration is performed along a path defined by vector
r(t)={x(t),y(t)}.
All the above analysis of a circulation of two-dimensional vector fields is easily transformed onto three-dimensional case, including the latest formula for a path integral with the only difference that vectors are dependent on three coordinates:
W[PQ] = ∫[PQ](F·dr),
where F = F(x,y,z) and
r = {x, y, z}.
Conservative Vector Fields
There are a few equivalent definitions of conservative vector field.
Here we will define a vector field as conservative if the above path integral (presented as a work done by moving a paper ship along some path from P to Q) depends only on the starting and ending points P and Q and is independent of which path from one to another we choose.
An immediate consequence of this is that a path integral along any closed loop is zero.
Indeed, choose two points on any closed loop, P and Q. Now we have two different paths from P to Q. Since integrals along both paths are the same, integral from P to Q along one of the paths is equal to integral from Q to P along the second path with an opposite sign:
∫[PQ](F·dr) = −∫[QP](F·dr)
The sum of these two integrals is a total integral on a closed loop, and it's equal to zero.
An equivalent definition of a conservative vector field F(x,y) is that it is a gradient of some scalar field f(x,y):
F(x,y) = grad f(x) = ∇f(x,y)
It can be proven that this definition is equivalent to the one above about path integral being dependent only on starting and ending points, each definition can be derived from the other.
The participating scalar function f(x,y) is called a potential for a given vector field F(x,y).
Curl of a Vector Field
By definition, a curl of a two-dimensional vector field at any point equals to a limit of this vector field's circulation along a closed path around that point, divided by the area enclosed in this path, assuming that this path's length and area it encloses tend to zero.
We leave open an issue about existence of this limit. Under general conditions of smoothness of the vector field this limit exists and, therefore, independent on how exactly we shrink the path around a point on a plane to reach the limit.
Let's find the curl analytically.
Choose a rectangular path ABCD around a point {x,y} of sizes Δx⨯Δy.
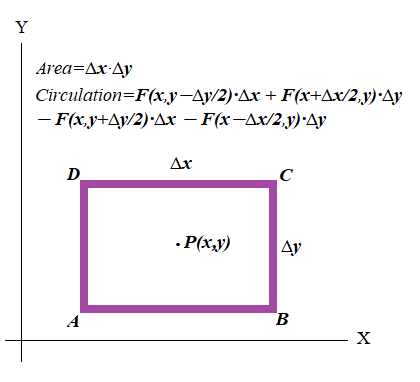
The choice of a rectangular form is related to ability to analyze separately X- and Y-components of the vector field with only one of them playing a role for each side of this rectangle.
Considering infinitesimal character of the sizes of this rectangle, we can assume that the X-component of the vector field Fx(x,y) is constant along the horizontal sides of a rectangle and equals to its value in the middle of a corresponding side, that is Fx(x,y−½Δy) for side AB and Fx(x,y+½Δy) for side CD.
This X-component should not participate in the calculation along vertical sides BC and DA, as it is perpendicular to them.
Similarly, we can assume that the Y-component of the vector field Fyy(x,y) is constant along the vertical sides of a rectangle and equals to its value in the middle of a corresponding side, that is Fy(x+½Δx,y) for side BC and Fy(x−½Δx,y) for side DA.
This Y-component should not participate in the calculation along horizontal sides AB and CD, as it is perpendicular to them.
Now the total circulation along our rectangular path is
W[ABCD] =
= Fx(x,y−½Δy)·Δx +
+ Fy(x+½Δx,y)·Δy −
− Fx(x,y+½Δy)·Δx −
− Fy(x−½Δx,y)·Δy
Signs of the members of the above sum depend on which vertex is a start of a path and which direction we choose. The formula above is related to point A as a start and counterclockwise movement along the path.
From the classical definition of a partial derivative for a function of two argument f(x,y)
∂f(x,y)/∂x =
= lim[f(x+Δx,y)−f(x,y)]/Δx
where lim is assumed as Δx→0.
Obviously, the same result is from a similar limit of
[f(x+½Δx,y)−f(x−½Δx,y)]/Δx
Therefore,
Fx(x,y+½Δy)−Fx(x,y−½Δy) ≅
≅ [∂Fx(x,y)/∂y]·Δy
Similarly,
Fy(x+½Δx,y)−Fy(x−½Δx,y) ≅
≅ [∂Fy(x,y)/∂x]·Δx
Using these, the circulation above equal to
[∂Fy(x,y)/∂x]·Δx·Δy −
− [∂Fx(x,y)/∂y]·Δx·Δy
Notice the area of a rectangle Δx·Δy as a multiplier in both component.
Therefore, dividing the circulation around an infinitesimal path around our point by the area encompassed by this path, we obtain the curl of the vector field
curl F(x,y) =
= ∂Fy(x,y)/∂x − ∂Fx(x,y)/∂y
We will use this definition in the next lecture that discusses curl of a two-dimensional vector field in more details.


No comments:
Post a Comment