Divergence
In this lecture we continue studying the characteristics of fields and, in particular, discuss another usage of symbol ∇ (nabla) that represents a set (or a triplet, or a pseudo-vector, or simply "vector") of three operators of partial differentiation, performed for each of the three dimensions of space we live in, in given Cartesian coordinates.
If needed, review the topic of partial derivatives in the "Calculus" part of the course "Math 4 Teens" on UNIZOR.COM.
We use the symbol ∇ as a shorthand for a triplet of operators of partial differentiation
∇ = {∂/∂x, ∂/∂y, ∂/∂z}
Previous lecture about gradient of a scalar field F(x,y,z) defined ∇F(x,y,z) as a "multiplication" of a "vector" ∇ by "scalar" F(x,y,z), resulting in a "vector", as traditional multiplication of a vector by a constant should:
∇F(x,y,z) =
= {∂F()/∂x, ∂F()/∂y, ∂F()/∂z}
The physical meaning of the gradient at any point {x,y,z} of a scalar field F(x,y,z) was a vector field (direction and magnitude at each point) of the greatest change of this field, thereby defining from a scalar field F(x,y,z) a vector field ∇F(x,y,z).
As an application of this concept, if F(x,y,z) represents an air density at point {x,y,z}, which is a scalar, the ∇F(x,y,z) represents the direction and magnitude of the most significant potential movement of the air, a vector, the main wind direction and its strength at each point.
The divergence is the result of a different operation with "vector" ∇.
Consider, again, an example of air distribution with different air density (and, therefore, pressure) in different areas of space. As a result, we can observe the direction and strength of a wind at any point - a vector field of air velocities (speed and direction of a wind) at each point.
The air goes from zones of higher density towards zones of lower density. While this process goes, the amount of air in a zone of higher density diminishes, while the amount of air in a zone of lower density increases until the density (and, therefore, pressure) equalizes. During this process the amount of air in a zone of average density in between the above two zones will remain steady, what air comes from a high density zone will go to a lower density.
The divergence of a vector field (for example, of a vector field of velocities of the wind at each point in space) quantitatively reflects the situation with air zones described above, showing the areas, from which air flows from and those it flows into.
Divergence is a scalar defined for each point of a vector field. It's positive for those areas, from which something (like air, or electrons, or energy) is flowing out, negative for areas receiving that something and zero if the amounts of coming into and going out are the same.
Let's approach this mathematically.
For each point {x,y,z} in space there is vector V(x,y,z) with projections on coordinate axes Vx(x,y,z), Vy(x,y,z) and Vz(x,y,z) so that the following vector equality is held:
V(x,y,z) = Vx(x,y,z)·i +
+ Vy(x,y,z)·j + Vz(x,y,z)·k
where i, j and k are unit vectors along X-, Y- and Z-axis.
Consider a parallelepiped ABCDEFGH centered at point P(x,y,z) and infinitesimal dimensions Δx⨯Δy⨯Δz.
Then coordinates of vertices are
A{x−½Δx,y−½Δy,z−½Δz}
B{x+½Δx,y−½Δy,z−½Δz}
C{x+½Δx,y+½Δy,z−½Δz}
D{x−½Δx,y+½Δy,z−½Δz}
E{x−½Δx,y−½Δy,z+½Δz}
F{x+½Δx,y−½Δy,z+½Δz}
G{x+½Δx,y+½Δy,z+½Δz}
H{x−½Δx,y+½Δy,z+½Δz}
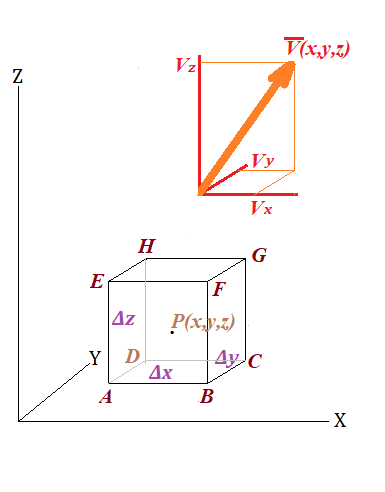
To bring some flavor into mathematics, let's use our analogy of the vector field V(x,y,z) as a direction and magnitude of the wind at point P(x,y,z).
To evaluate the air contribution by this wind into point P(x,y,z), we will calculate how much air coming in and going out of the parallelepiped ABCDEFGH per unit of time and take its limit, as the dimensions of this parallelepiped are infinitesimal.
We will consider three major directions along the three axes of the coordinate system and coordinate representation of the vector V(x,y,z).
Projection of the vector V(x,y,z) on the X-axis Vx(x,y,z)·i brings air into our parallelepiped through its left side and takes the air out through its right side.
In the middle of the left side this projection is Vx(x−½Δx,y,z)·i.
In the middle of the right side this projection is Vx(x+½Δx,y,z)·i.
Since we assume that our parallelepiped has infinitesimal dimensions, we can assume that the projection of the vector V(x,y,z) on the X-axis at each point of the left side ADHE is the same as in the middle of this side at point {x−½Δx,y,z}.
Similarly, we assume that the projection of the vector V(x,y,z) on the X-axis at each point of the right side BCGF is the same as in the middle of this side at point {x+½Δx,y,z}.
The amount of air moving out through the right side of a parallelepiped is proportional to the average speed of wind at the right side Vx(x+½Δx,y,z) times the area of the right side Δy·Δz.
Similarly, the amount of air moving in through the left side of a parallelepiped is proportional to the average speed of wind at the left side Vx(x−½Δx,y,z) times the area of the left side Δy·Δz.
The net result of air moving in and out of the parallelepiped along the X-axis is proportional to
Ax(x,y,z) = [Vx(x+½Δx,y,z) −
− Vx(x−½Δx,y,z)]·Δy·Δz
Recall from the calculus the following property of differentiable function f(x):
f(b) − f(a) = df(c)/dx · (b−a)
where point c is somewhere between a and b.
If a→b (that is, b−a is an infinitesimal variable), c also tends to a (or b) and
df(c)/dx ≅ df(a)/dx ≅
≅ df(b)/dx ≅ df(½(a+b))/dx.
Using this property in our case with a=x−Δx and b=x+Δx, with Δx infinitesimal, we derive
Vx(x+½Δx,y,z) −
− Vx(x−½Δx,y,z) ≅
≅ ∂Vx(x,y,z)/∂x · Δx
Now the expression for an amount of air accumulated in the vicinity of point {x,y,z} is
Ax(x,y,z) ≅
≅ ∂Vx(x,y,z)/∂x · Δx·Δy·Δz
Since Δx·Δy·Δz is the volume of our parallelepiped, dividing both sides of the equation above by it will give a change (positive for increment or negative for decrement) of air density in the infinitesimal neighborhood of point {x,y,z}, contributed by a component of the vector field in the X-axis direction.
Dx(x,y,z) ≅ ∂Vx(x,y,z)/∂x
Analogously, contribution to air density by Y-component of the vector field V(x,y,z) is
Dy(x,y,z) ≅ ∂Vy(x,y,z)/∂y
And Z-component of this vector field adds
Dz(x,y,z) ≅ ∂Vz(x,y,z)/∂z
The combined contribution of air density will be a sum of these individual contributions, a divergence (div) of the vector field V(x,y,z):
divV(x,y,z) = ∂Vx(x,y,z)/∂x +
+ ∂Vy(x,y,z)/∂y + ∂Vz(x,y,z)/∂z
To simplify this expression, ∇ to the rescue.
Considering ∇ as a "vector"
∇ = {∂/∂x, ∂/∂y, ∂/∂z}
and V(x,y,z) being a vector in coordinate representation
{Vx(x,y,z),Vy(x,y,z),Vz(x,y,z)}
the expression for a divergence above can be represented as a scalar (dot) product of these two "vectors":
divV(x,y,z) = ∇ · V(x,y,z)
Other examples of the usage of a concept divergence are: divergence of the electric field (not zero where there are electric charges, see the First Maxwell equation),
divergence of the magnetic field (always zero, see the Second Maxwell equation),
divergence of the gravitational field (non-zero inside any material object, zero in vacuum),
and any others, where it makes sense to talk about vector field.


No comments:
Post a Comment