For a short introduction to the International System of units (SI) see the previous lecture "SI Intro & Time" within this topic.
Luminosity Units
The purpose of this lecture is to introduce a measure of luminosity (luminous intensity) of some source of light.
This involves measuring the intensity of the source of light, spectral composition of this light, direction the energy of light is propagated and sensitivity of human eyes to different types of light.
Seems to be a very complicated task.
Let's start with a simpler concept of radiant flux. This is just an amount of energy emitted by some source of electromagnetic oscillations per unit of time, and it's measured in joules (watt per second).
The next step is a concept of luminous flux. It's different from radiant flux in what is related to a human eye's sensitivity to different wave lengths of electromagnetic oscillations.
The specialists that researched the eye sensitivity to light came up with a luminosity function that is an average among people and standardized distribution of eye's sensitivity to different wave lengths of light. This function is, obviously, zero for those wave lengths outside of a visible spectrum. Within a visible spectrum it has a bell shape with the maximum around wave length of green light - the light to which our eyes are most sensitive.
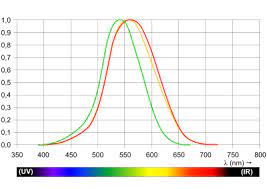
Two distribution functions on the above picture are for different lighting conditions with the red curve usually used for practical purposes.
Using this function, we define luminous flux Φlum(λ) of a monochromatic light of specific wavelength λ as a product of its radiant flux Φrad(λ) by luminosity function y(λ) for that wavelength.
For light that encompasses the whole spectrum of wavelengths we integrate the luminous flux for each wavelength to obtain the total luminous flux Φlum
Φlum = ∫[0,∞]Φrad(λ)·y(λ)·dλ
The unit of luminous flux is called lumen (lm). Essentially, it's joules per second factored by the luminosity function.
Now let's talk about a direction of light since the light can be propagated differently in different directions.
Recall that angles on a plane are measured in radians (rad) with 1 rad being such an angle that, if used as a central angle in a circle of a radius R, will be subtended by an arc of the length R.
Solid angles in three-dimensional space are measured in steradians (sr) with 1 steradian (1 sr) being a part of space inside a cone such that, if this cone is placed inside a sphere with its vertex coinciding with the center of a sphere, it will be subtended by a part of sphere's surface of the area R².
Light from a source propagates in all directions. To deal with a possibility to emit different by brightness light in different directions we introduce luminosity as luminous flux per the unit of solid angle, steradian.
The unit for luminosity is called candela and
1 candela (cd) = 1 lumen (lm)
per 1 steradian (sr)
Historically, candela was, approximately, a luminosity of a candle of certain characteristics (size, shape, composition).
Realizing imperfectness of such a definition, later on candela was redefined as 1/60th of the luminosity of 1 cm² of surface of melting platinum.
Finally, to get more precise definition, it was decided to define 1 candela as a base SI unit independently of eye sensitivity only for a specific monochromatic light of frequency 540·1012 Hz (which is the light of the wavelength of about 555 nm - the green-yellow color, where eye sensitivity of most people is at maximum) as the one emitting radiant intensity in a particular direction equal to 1/683rd joule.
The above definition gives a new unit of luminosity, candela (cd), about the same numerical value as it was defined previously, but puts it on a precise foundation.
Introduction of any particular luminosity function defines candela for other wavelengths.
Now if the light of 1 candela (abbreviation 1 cd) of the above frequency is uniformly propagated in all directions (there are 4π steradian in a sphere because its surface is 4πR²), the total radiant intensity will be
1 cd · 4π sr = 4π lumen (lm)
As an illustration, the luminosity of 800 candela can be obtained by an incandescent lamp that consumes 60 watt of energy per hour or by a fluorescent lamp consuming about 14 watts per hour, or by an LED lamp consuming about 10 watts per hour.


No comments:
Post a Comment