Fission
Atoms of certain heavy elements, like uranium-235 or plutonium-239 are not very stable and can split into lighter elements if sufficient external force (like an absorption of a neutron) is applied.
This is called a nuclear fusion.
Below is one of the possible kind of a nuclear fission occurred when a neutron is captured by a nucleus of uranium-235.
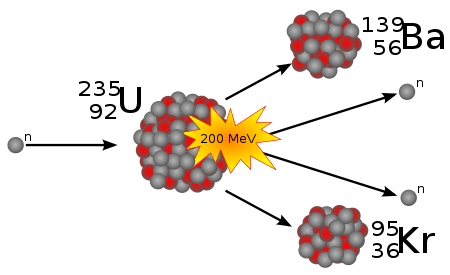
This reaction can be described by a nuclear equation
0n1 + 92U235 →
→ 56Ba139 + 36Kr95 + 2·0n1
Indeed, the number of protons on the left side of this equation is 0+92=92, which corresponds to this number on the right side 56+36+2·0=92.
The atomic number (number of protons and neutrons) on the left is 1+235=236, which corresponds to the right side 139+95+2·1=236.
The mass of a nucleus of uranium-235 is 235.043928 atomic mass units (amu).
The mass of a nucleus of barium-139 is 138.908841 amu.
The mass of a nucleus of krypton-95 is 94.939711 amu.
Neutron's mass is 1.007 amu.
The total mass of particles on the left side of equation is
1.007 + 235.043928 ≅
≅ 236.051 amu
The total mass of particles on the right side of equation is
138.908841 + 94.939711 +
+ 2·1.007 ≅ 235.863 amu
Mass Defect & Energy
As we see, in this reaction the resulting mass of fission components is less than the original mass. The difference in mass of 0.188 amu is the mass defect.
Where did this extra 0.188 amu go?
It's converted into energy released during this process of fission.
To calculate the energy that is released by the above process of fission, we use the famous Einstein's formula
E = m·c²
substituting the mass defect of 0.188 amu for mass m in this formula, where
1 amu ≅ 1.66·10−27 kg
and speed of light in vacuum
c≅3·108 m/sec.
The resulting amount of energy EU235 released by the above reaction of fission of a single nucleus of uranium-235 is
EU235 ≅
≅ 0.188·1.66·10−27·9·1016 ≅
≅ 2.809·10−11 J (joules)
An atom of uranium has mass of, approximately,
That means, there are, approximately, 0.253·1022 atoms in 1 gram of uranium.
Let's see how much energy can be released if all nuclei in the 1 gram of uranium-235 split into peaces as described above.
E1gU235 ≅
≅ 2.809·10−11·0.253·1022 ≅
≅ 0.711·1011 J ≅ 20,000 kwh
Burning one gallon of gasoline produces about 4 kilowatt hours of energy.
Therefore, one gram of uranium-235, if all its atoms go through a fission process described above, produce an amount of energy equivalent to about 5,000 gallons of gasoline.
Fission Variants
The described above reaction of fission of uranium-235 is not the only one possible.
Under different environmental conditions and just by chance the fission of uranium-235 can produce different resulting components.
Here are a few examples.
0n1 + 92U235 →
→ 56Ba144 + 36Kr89 + 3·0n1
where different isotopes of barium and krypton are produced.
0n1 + 92U235 →
→ 40Zr94 + 52Te139 + 3·0n1
where zirconium and tellurium are produced.
0n1 + 92U235 →
→57La139+42Mo95+2·0n1+7·e−
where 7 neutrons transformed into proton+electron pairs.
The components of fission can be different, the different is also an amount of energy released in each separate case.
Chain Reaction
The above examples of fission of a single nucleus of uranium-235, when it absorbs a single neutron, show that these reactions can produce more neutrons that one. If these two or three neutrons, in turn, are absorbed by other nuclei, those will split as well, producing more neutrons.
Under certain circumstances this might cause a chain reaction of fission.
These circumstances include, primarily, the amount of uranium-235, its purity and shape.
The picture below schematically shows how a fission of a single nucleus can cause a chain reaction of other nuclei around it, producing all kinds of fission products and new neurons that cause more fission reactions.
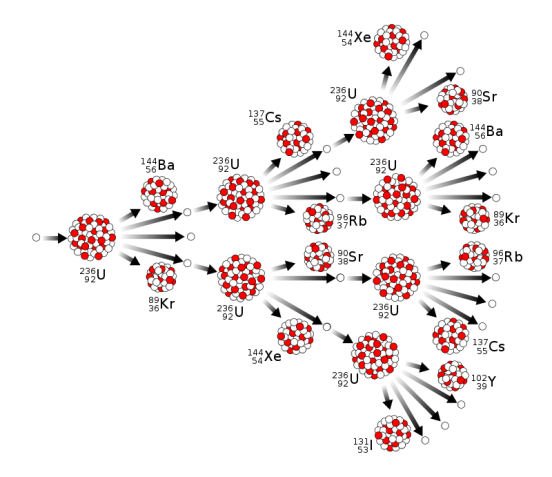
There is a concept of a critical mass for each element that can undergo the fission. Two primary elements used for peaceful (producing energy) and not peaceful (to make a bomb) purposes are
uranium-235 (92U235) and
plutonium-239 (94Pu239).
Critical mass
for uranium-235 is 47 kg,
for plutonium-239 it is 10 kg.
These numbers are approximate and are based on normal temperature, average density and spherical shape of a nuclear fuel mass.
Of course, the purity is also playing an important role, the greater the purity - the smaller critical mass required to initiate a chain reaction. For example, if uranium-235 represents only 20% of the total mass, the critical mass would be over 400 kg.
If the mass is less than critical, neutrons produced by a reaction of fission might just fly away, not absorbed by another nucleus.
If some kind of neutron reflectors are positioned around a mass of nuclear fuel, it increases the probability of such an absorption and decreases the critical mass, sometimes by a factor of 2.
Without any preventive measure, the chain reaction causes an explosion. That's how atomic bombs are working.
On the other hand, using neutron absorbers embedded into the mass of uranium-235 or plutonium-239, like graphite or boron, reduces the number and slows down the neutrons emitted by fission, which slows down or stops the chain reaction. That's how the nuclear power stations work.


No comments:
Post a Comment