Algebra+ 03: UNIZOR.COM - Math+ & Problems - Algebra

Notes to a video lecture on http://www.unizor.com

Algebra+ 03

Problem A

Let n be any natural number/

Define two functions of n:
F(n) = 1 − 1/2 + 1/3 -…+
+ 1/(2n-1) − 1/2n
and
G(n) = 1/(n+1) + 1/(n+2) +…+
+ 1/(2n-1) + 1/2n

Prove that for any natural n the following equality is true:
F(n)=G(n).

For example, you can manually check the following equalities:
for n=1 (2n=2):
1 − 1/2 = 1/2
for n=2 (2n=4):
1 − 1/2 + 1/3 − 1/4 =
= 1/3 + 1/4
for n=3 (2n=6):
1− 1/2 + 1/3 − 1/4 +
+ 1/5 − 1/6 =
= 1/4 + 1/5 + 1/6


Answer A

Here is a straight forward proof by induction.

Check it for n=1:
F(1) = 1−1/2 = 1/2
G(1) = 1/2
As we see, F(1) = G(1)

Assume, F(n)=G(n).
Let's switch to n+1
F(n+1) =
= F(n) + 1/(2n+1) − 1/(2n+2)
G(n+1) = G(n) − 1/(n+1) +
+ 1/(2n+1)+1/(2n+2)

When we switch from n to n+1, function F(n) has changed by
f(n+1) = 1/(2n+1) − 1/(2n+2)
So, F(n+1)=F(n)+f(n+1).

Analogously, function G(n) has changed by
g(n+1) = −1/(n+1) +
+ 1/(2n+1) + 1/(2n+2)
So, G(n+1)=G(n)+g(n+1).

If f(n+1), an increment of F(n), and g(n+1), an increment of G(n), are equal, assuming F(n)=G(n), we can conclude that F(n+1)=G(n+1), which proves that F(n)=G(n) for any natural number n.

Let's check the equality
f(n+1) = g(n+1)

Indeed, transforming an expression to a common denominator, we get
f(n+1) = 1/[(2n+1)·(2n+2)]

For g(n+1) the common denominator is
(n+1)(2n+1)(2n+2)
The numerator is
−(2n+1)(2n+2)+(n+1)(2n+2)+
+(n+1)(2n+1) =
= −4n² − 2n − 4n − 2 +
+ 2n² + 2n + 2n + 2 +
+ 2n² + n + 2n + 1 =
= n+1

Dividing this numerator of g(n+1) by its denominator obtained above and cancelling n+1 from both, we will get
g(n+1) = 1/[(2n+1)(2n+2)]

This is exactly what we obtained for f(n+1).

END OF PROOF


Problem B

Two cars are approaching an intersection on two perpendicular roads.
In the beginning at time t=0 car #1 is at distance a from the intersection.
The car #2 (on a perpendicular road) at t=0 is at distance b from the intersection.
Both cars move with the same speed V.
For traffic safety, assume that a≠b, so there will be no collision.


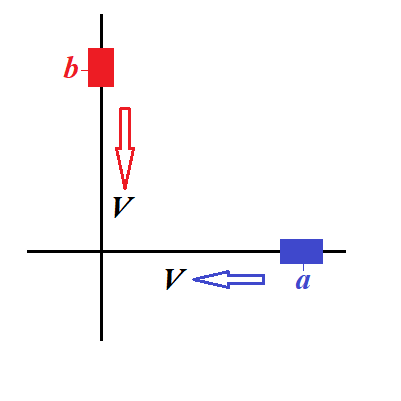
At what time the distance between the cars will be minimal and what that minimal distance will be?


Answer B

Let d(t) be a distance between the cars at any moment t.
Then
d²(t) = (a−v·t)² + (b−v·t)²

Minimum of d(t) and d²(t) occur for the same moment in time t.
So, our task is to find minimum of d²(t), which is a quadratic function of t.

The time when the cars are closest to each other is
t_min = (a+b)/(2V)

The closest distance between the car at that time is
d_min = |a−b| /√2