Geometry+ 05: UNIZOR.COM - Math+ &Problems - Geometry

Notes to a video lecture on http://www.unizor.com

Geometry+ 05


Problem A

Construct a quadrilateral ABCD by its 4 sides AB, BC, CD, DA and an angle φ between opposite sides AB and CD.

Hint A

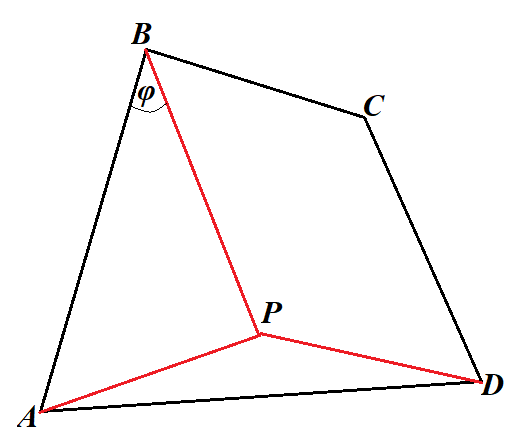
Find point P such that BP is parallel and congruent to CD.
Consider ΔABP.


Problem B

Given a circle of radius R and n-sided regular polygon inscribed into it.
Let P be any point on this circle.
Find a sum of squares of distances from this point P to all vertices of a polygon.

Hint B
(a) Geometrical solution for even number n of vertices of a regular polygon can be obtained by adding pairs of distances from P to i^th and (i+½n)^th vertices.
(b) General solution can be obtained if using vectors from the center of a circle to all its vertices and to point P.

Answer
Sum of squares of distances from point P to all vertices of a polygon equals to 2nR².


Problem C

Given an equilateral triangle ΔABC.
Extend side AC beyond vertex C to point D and build another equilateral triangle CDE with point E on the same side from AD as point B.
Connect points A and E. Let point M be a midpoint of segment AE.
Connect points B and D. Let point N be a midpoint of segment BD.

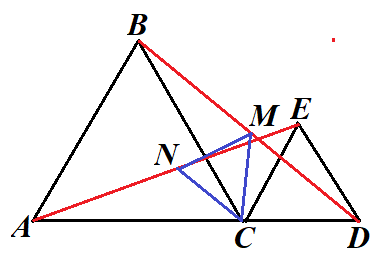
Prove that triangle ΔCMN is equilateral.

Hint C
Triangles ΔACE and ΔBCD are congruent.