Geometry+ 06: UNIZOR.COM - Math+ & Problems - Geometry

Notes to a video lecture on http://www.unizor.com

Geometry+ 06

Problem A

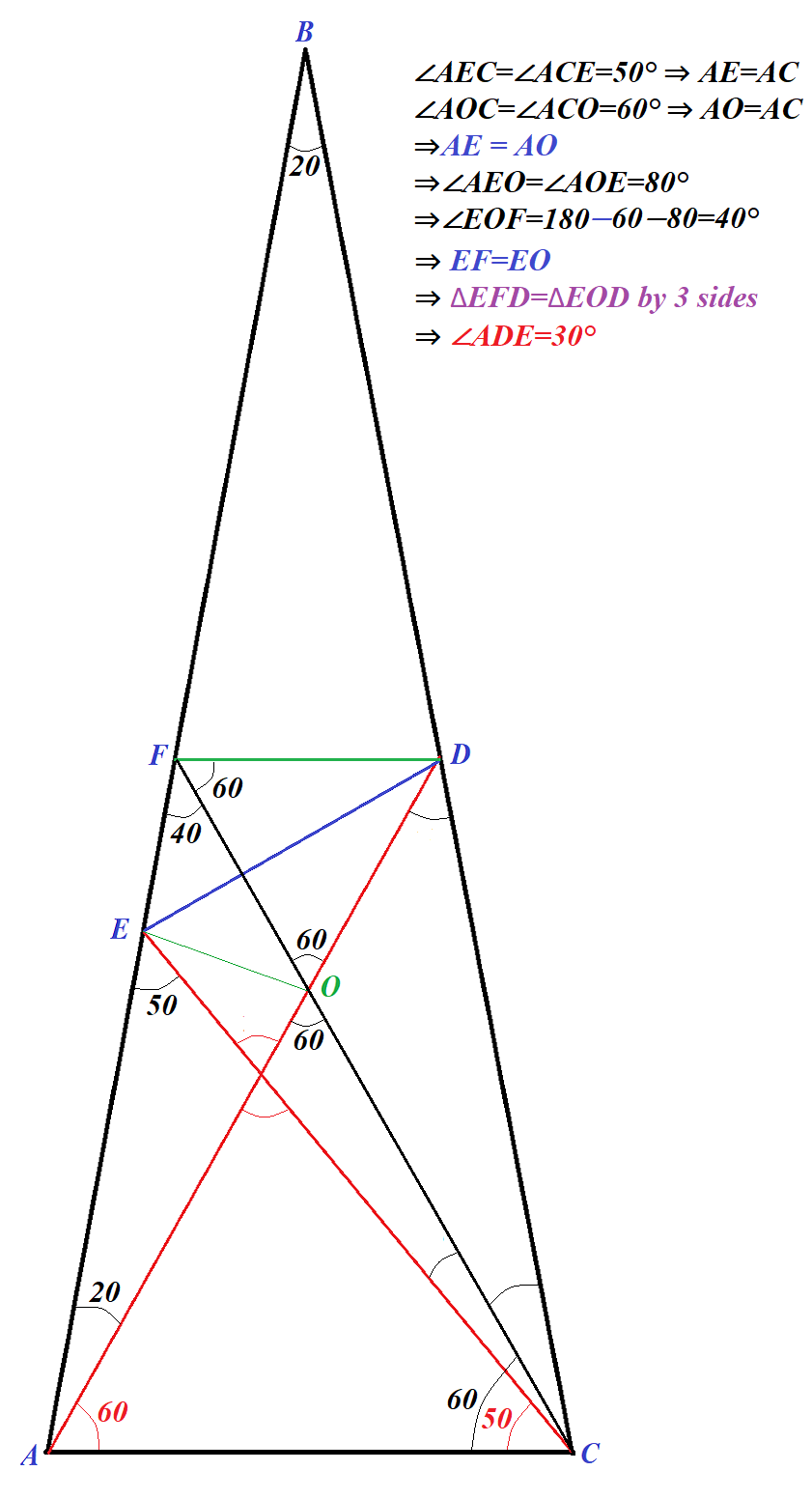
Given an isosceles triangle ΔABC with AB=BC and ∠ABC=20°.
Point D on side BC is chosen such that ∠CAD=60°.
Point E on side AB is chosen such that ∠ACE=50°.
Find angle ∠ADE.

Solution A



Problem B

Given two triangles ΔA₁B₁C₁ and ΔA₂B₂C₂ with the following properties:
(a) side A₁B₁ of the first triangle equals to side A₂B₂ of the second;
(b) angles opposite to these sides, ∠A₁C₁B₁ and ∠A₂C₂B₂, are equal to each other;
(c) bisectors of these angles, C₁X₁ and C₂X₂, are also equal to each other.

Prove that these triangles are congruent.

Proof
Put side A₁B₁ on top of A₂B₂ and draw a circle around ΔA₁B₁C₁.
Obviously, point C₂ would lie on this circle because of equality of angles opposite to equal sides.
Assume that points C₁ and C₂ do not coincide.
Extend bisectors C₁X₁ and C₂X₂ to intersection with a circle at point P. It must be the same point for both bisectors because each divides the arc ⌒A₁B₁ in half.

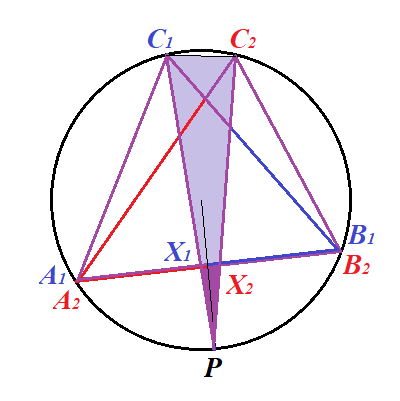
First, let's prove that triangle ΔPC₁C₂ is similar to triangle ΔPX₁X₂
Our proof will be based on congruency of two angles of one triangle to two corresponding angles of another.
For brevity, when we use an expression "angle is measured by an arc (or a fraction of it)", we mean that this angle is equal to a central angle subtended (supported) by this arc (or a fraction of it).

We will also use known theorems of Geometry:
(Theorem 1) An angle inscribed into a circle (that is, formed by two chords with one common point on a circle) is measured by half an arc it cuts from a circle by its two rays.
(Theorem 2) An angle formed by two chords intersecting inside a circle is measured by half of a sum of two opposite arcs these chords cut.
These theorems were presented in UNIZOR.COM - Math 4 Teens - Geometry - Circles - Mini Theorems 1 and ...Mini Theorems 2.

1. ∠PC₁C₂ is measured by half of sum of arcs ⌒C₂B₂ and ⌒B₂P;
∠PX₂A₂ is measured by half of sum of arcs ⌒C₂B₂ and ⌒PA₂;
but arcs ⌒B₂P and ⌒PA₂ are equal, from which follows that
∠PC₁C₂ equal to ∠PX₂A₂.

2. ∠PC₂C₁ is measured by half of sum of arcs ⌒C₁A₂ and ⌒A₁P;
∠PX₁B₁ is measured by half of sum of arcs ⌒C₂B₂ and ⌒PA₂;
but arcs ⌒B₂P and ⌒PA₂ are equal, from which follows that
∠PC₁C₂ equal to ∠PX₂A₂.

Since two angles of ΔPC₁C₂ are congruent to two angles of ΔPX₁X₂, these triangles are similar.
Consequently, their sides are proportional
PC₁/PX₂ = PC₂/PX₁

If angle bisectors C₁X₁ and C₂X₂ are equal, segments C₁P and C₂P must be equal to preserve the proportionality of corresponding sides of triangles ΔPC₁C₂ and ΔPX₁X₂.
Indeed, if C₁X₁=C₂X₂=d, PX₁=x₁ and PX₂=x₂, then
(d+x₁)/x₂ = (d+x₂)/x₁
⇒ d·x₁+x₁² = d·x₂+x₂²
⇒ d·(x₁−x₂) = (x₂−x₁)·(x₁+x₂)
⇒ x₁ = x₂, because otherwise d would be negative −(x₁+x₂).

From C₁P = C₂P follows
⇒ ⌒C₁A₁P = ⌒C₂B₂P
⇒ ⌒C₁A₁ = ⌒C₂B₂
⇒ C₁A₁ = C₂B₂
Analogously,
⇒ C₁B₁ = C₂A₂
which proves that triangles ΔA₁B₁C₁ and ΔA₂B₂C₂ are congruent by three sides.