Current in a Loop: UNIZOR.COM - Physics4Teens - Electromagnetism - Magne...

Notes to a video lecture on http://www.unizor.com



Magnetism of Electric Current in a Loop



Let's recall some general considerations of any field produced by a
point-source (like gravitational or electrostatic) and the force it
exerts at certain distance from its center.



In three-dimensional space the field influence is spreading around in
all directions from its center, and at any given time it reaches and
spreads over a sphere of the area 4πR², where R is the radius of this sphere.



This important consideration prompted the dependency between the
magnitude of the field force at any point in space and inverse of a
square of a distance between this point and the source of a field.

This dependency exists in all laws related to fields we studied, and it's true for magnetic field as well.



There is, however, an important complication with the sources of
magnetic field. Strictly speaking, they are not and theoretically cannot
be just points, because they always have a characteristic of the
direction. If it's a permanent magnet, there is a North pole to South
pole direction. If the source is a direct current, there is a direction
of electrons that causes the existence of a magnetic field.

So, besides the distance from the source of a magnetic field, another
important aspect that influences the magnetic field is how the point of
measuring the magnetic field is positioned relatively to a direction of
the electric current at the source of a field.



Consider measuring a strength of a magnetic field at point P on the following picture.



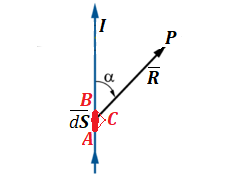
Here an infinitesimal segment AB of the length dS of a wire with an electric current I produces a magnetic field that we are measuring at point P. From the viewpoint of point P segment AB is visible at an angle and seems having the size of a segment BC that is perpendicular to a radius-vector R from the source of magnetic field segment AB to the point of measuring P.



Simple geometry gives the visible from point P length of segment AB - the length of BC, which is the length of AB multiplied by sin(α).



With this correction to a simple dependency of the strength of magnetic
field on the inverse square of a distance from the field source we can
represent the magnitude of the vector of magnetic field strength or
intensity at point P as

dB = k·I·dS·sin(α) / R²

The constant k in SI units equals to μ₀/(4π), where μ₀ is the permeability of free space. So the formula for a magnitude of the strength of magnetic field looks like this:

dB = μ₀·I·dS·sin(α) / (4πR²)



The vector of force has magnitude and direction. The magnitude was
evaluated above. The direction of this force, based on experimental
data, is always perpendicular to both the direction of the current I and the direction of the radius-vector from the source of magnetic field to a point of measurement P.



This allows us to express the vector of magnetic field intensity B in a form of a vector product

B = μ₀·I·dS ⨯ r / (4πR²)

where r is a unit vector in the direction from the source of magnetic field segment AB to the point of measurement P.

Equivalent formula is

B = μ₀·I·dS ⨯ R / (4πR³)



Let's apply this formula to calculate the magnetic field intensity and direction in a center of a circular wire loop of radius R with electric current I running through it.



We divide the circular wire loop into infinitesimal segments of the length dS. Fortunately, all radiuses from any such segment to a center of a loop are perpendicular to these segments, so sin(α)=1 in the above formula for a magnitude of the intensity vector.



The magnetic field intensity B from each segment equals to

dB = μ₀·I·dS / (4πR²)

The direction of this force is perpendicular to both radius to a segment dS
and to a segment itself. That is, it should be perpendicular to a plane
of the wire loop, that is the vector of magnetic field force in a
center of a wire loop is always directed perpendicularly to the loop.

Since it's true for any segment dS, we can just add all the forces from all the segments, that is, we have to integrate the above expression by S along the whole circle from 0 to 2πR.

The only variable in the above expression is dS, so the result is

B = ∫_[0,2πR] μ₀·I·dS/(4πR²) =

= 2πR·μ₀·I/(4πR²)= μ₀·I/(2R)