Notes to a video lecture on http://www.unizor.com
Self-Induction
Let's study the process of increasing the direct electric current in a
wire loop that is connected to a source of a direct electricity (like
battery) that generates electromotive force of voltage U0.
This increase might be attributed to a decrease in resistance in this
loop. For example, if the wire loop was initially disconnected from a
source of electricity and we connected it, flipping some switch, the
resistance is changing from being practically infinite to some value R during a fraction of a second and the electric current would grow from zero to some value
I = U/R (Ohm's Law).
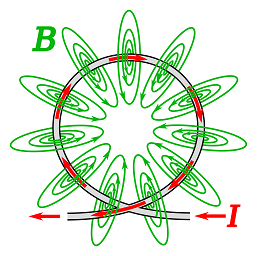
The first thing that we can observe is that there is a magnetic field
generated by an electric current with magnetic field lines going through
a loop, thus effectively making it a magnet.
The next thing we note is that the intensity of a magnetic field
generated by an increasing direct current is also increasing with the
current because of their relationship that we have described in the
lecture about magnetism of an electric current loop.
In the center of an ideally circular loop this intensity, as we calculated in that lecture, is
B = μ0·I/(2R)
where
μ0 is permeability of space,
I is the current in a wire loop,
R is the radius of a wire loop.
At other points around the wire the intensity of a magnetic field also
increases proportionally to the electric current in a wire. Even if the
shape of our wire loop is not ideally circular, the proportionality of
intensity of a magnetic field at any point to an electric current would
still be held, because each infinitesimal segment of a wire creates its
own magnetic field and the magnetic field intensity is an additive
function, that is, produced by two sources, intensities from each are
added as vectors, resulting in a combined intensity.
As a result, the magnetic flux going through a wire loop increases proportionally to an increase in electric current.
Now recall the Faraday's Law of magnetic induction. It states that changing magnetic flux going through an electric circuit generates electromotive force (EMF) proportional to a rate of change of the magnetic flux, where rate of change means a change per unit of time, which, using mathematical language, is the first derivative of a variable magnetic flux by time.
Let's ignore for now the signs of the rate of change of the magnetic flux and the EMF, then the Faraday's Law can be represented as
U = dΦ/dt
where
U is the absolute value of a magnitude of the generated EMF,
Φ is magnetic flux,
t is time,
dΦ/dt is the rate of change of magnetic flux (first derivative of magnetic flux by time), taken as an absolute positive value.
From
(1) the proportionality of a magnetic field intensity at any point around a wire to an electric current going through a wire,
(2) definition of magnetic flux and
(3) the Faraday's Law
follows that the increasing electric current, causing an increasing
magnetic flux going through a circuit (so, the first derivative of a
magnetic flux is positive), generates a secondary EMF in
the circuit that is proportional to a rate of change of a magnetic flux,
which, in turn, is proportional to a rate of change of the electric
current in a loop.
So, generated (induced) secondary EMF is proportional to a rate of change of an electric current in a loop.
This induced secondary EMF causes the secondary electric current in a loop that interferes with the original electric current.
The process of interference of two electric currents, varying original
one and that caused by a change of magnetic field flux, is called self-induction.
Now let's talk about the direction of that secondary current from the position of the Law of Energy Conservation.
If the secondary current flows in the same direction as the increasing
original one, the rate of change of electric current in a loop will
increase, causing a greater rate of change of the magnetic flux, causing
even greater rate of change of the electric current flowing through a
wire, causing even greater flux etc. This is a perfect source of free
energy, so it cannot be true.
Indeed, the secondary electric current must be directed opposite to an
increasing original one, thus slowing the rate of increase.
The EMF generated by self-induction is opposite to the one that originated the increase in the electric current in a loop.
As a practical implication of this principle, when we switch a lamp on,
and the time a switch actually closes the circuit is, for example 0.01
sec, the electric current in a circuit will not reach its maximum during
this exact time, but later, like during 0.02 sec, because of
self-induction that slows the increase of amperage.
Let's consider the process of decreasing of the electric current in a
loop, like when we disconnect a wire from a primary source of
electricity.
Decreasing electric current in a wire loop causes proportional decrease
of a magnetic field intensity at any point around a wire.
This, in turn, causes proportional decrease of magnetic flux flowing through a wire loop with rate of change (first derivative of flux by time) negative.
Negative rate of change of magnetic flux causes the generation of secondary (induced) EMF in a wire, that results in a secondary electric current, that interferes with the decreasing primary one.
Let's analyze the direction of this secondary electric current.
Above, when the primary electric current was increasing and the rate of change of magnetic flux was positive,
we concluded that induced EMF causes the secondary electric current to
go in the opposite to primary direction to preserve the Law of Energy
Conservation.
In a case of decreasing primary electric current we see that the
magnetic flux flowing through a wire loop is decreasing, it's rate of
change (first derivative) is negative, so the secondary (induced) EMF must be directed opposite to the one generated by an increasing primary electric current.
Therefore, if in the case of increasing primary electric current the secondary EMF "worked" against the electric current,
generating a secondary current in a direction opposite to an increasing
primary one, in the case of decreasing primary current the secondary (induced) EMF generates the secondary current in the same direction as a decreasing primary current, "helping" the decreasing primary current, prolonging the decrease.
So, in both cases the secondary (induced) EMF works opposite to a rate of change of the magnetic flux going through a wire loop.
When the magnetic flux increases, the induced EMF generates an
electric current in the opposite direction to a primary one, thus
slowing the rate of increase of the electric current and, therefore,
against the rate of increase of the magnetic flux.
When the magnetic flux decreases, the induced EMF generates an
electric current in the same direction as a primary one, thus slowing
the decrease of the electric current and, therefore, against the rate of
decrease of the magnetic flux.
The above considerations are the primary reason why the Faraday's Law is expressed as
U = −dΦ/dt
where the minus sign signifies that the induced EMF works against the rate of change of a magnetic flux.


No comments:
Post a Comment