Notes to a video lecture on http://www.unizor.com
Induced Variable EMF
The most important fact about electromagnetic induction is that variable magnetic flux Φ(t) going through some wire frame generates in it an electromotive force (EMF) U(t) proportional to a rate of change of the magnetic flux and oppositely directed.
U(t) = −dΦ(t)/dt
Let's apply it to the following experiment.

The experiment consists of a permanent magnet moving into a wire loop,
as shown on the above picture, with different positions of a wire loop
relatively to a magnet at different times marked as t=1, t=2 etc.
At t=1 a magnet is still outside of the area of a wire loop, facing a loop with its North pole.
At t=2 a North pole of a magnet enters the area of a wire loop.
At t=3 a magnet covered half of its way through a wire loop, so the loop is positioned around a midpoint of a magnet.
At t=4 a South pole of a magnet leaves the area of a wire loop.
At t=5 a magnet is completely out of the area of a wire loop.
While the magnet is far from a wire loop (even before time t=1), practically no electricity can be observed in a wire loop. There are two reasons for it.
Firstly, the magnetic field is weak on a large distance.
Secondly, the direction of magnetic field lines in an area where a
wire loop is located at a large distance from a magnet is practically
parallel to the movement of a magnet (or movement of a wire loop
relative to a magnet). In this position a wire crosses hardly any
magnetic field lines and, consequently, the magnetic flux going through a wire loop is almost constant. Hence, the rate of the magnetic flux change is almost zero and no EMF is induced.
As we move the magnet closer (time t=1), its magnetic field in the area of a loop is increasing in magnitude and the angle between the magnetic field lines in the area of a wire loop and the direction of a wire loop relative to a magnet becomes more and more perpendicular. The magnetic flux going through a wire loop is increasing and, consequently, the EMF induced in a wire becomes more noticeable.
At time t=2 the magnitude of the magnetic field reaches
its maximum, the direction of magnetic field lines crossed by a wire
loop is close to perpendicular to a relative movement of a wire. The
magnetic flux changes rapidly and induced EMF in the wire is strong.
At time t=3 the wire loop is at the midpoint of a magnet.
The strength of a magnetic field at this position is very weak, magnetic
field lines are practically parallel to the relative movement of a
wire, and no noticeable EMF is generated.
At time t=4 the situation is analogous to that of t=2
with only difference in the direction of the magnetic field lines. Now
the wire is crossing them in the opposite direction, which causes the
induced EMF to have a different sign than at time t=2.
After that, at time t=5 the induced EMF is diminishing in magnitude and becomes almost not noticeable.
In the next experiment we replace the permanent magnet with a wire loop A
with direct current running through it. As we stated many times, the
properties of a wire loop with direct electric current going through it
are similar to those of a permanent magnet.
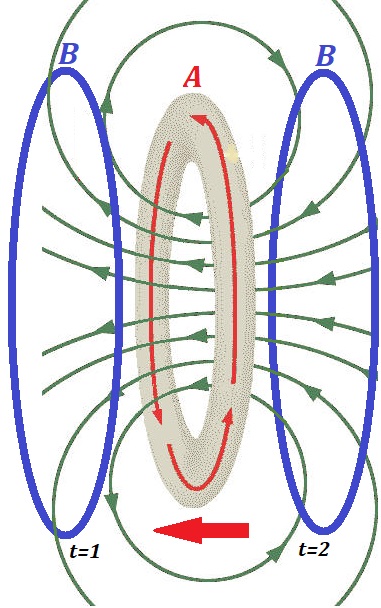
So, if we move the wire loop A with the direct current closer and closer to a wire loop B not connected to any source of electricity, the magnetic flux going through a wire loop B will be changing and, similarly to the first experiment, the induced EMF will be observed in this wire loop B.
Two positions of the loop B relative to a wire loop A are pictured above at times t=1, when wire loop A is very close to wire loop B, and t=2, when wire loop A has passed the location of wire loop B.
Similar considerations lead us to conclude that at times t=1 and t=2 the rate of change of magnetic flux through wire loop B will be the greatest and, consequently, the induced EMF in it will be the greatest.
However, these two EMF's will be opposite in direction because the
direction of crossing the magnetic lines will be opposite - at time t=1 magnetic lines are directed from inside wire loop B, but at t=2 the lines are directed into inside loop B.
In both experiments above the most important is that variable magnetic
flux going through a wire loop, not connected to any source of
electricity, induces the EMF in it.
Our third and final experiment is set as the second, except, instead of using constant direct current in the wire loop A and moving it through wire loop B to cause changing magnetic flux, we will keep the wire loop A
stationary, but will change the intensity of its magnetic field by
changing the magnitude of the electric current going through it.
The result of changing electric current I(t) going through wire loop A of radius R (as a function of time t) is changing magnetic field vector B(t) it produces.
We did calculate the value of the intensity of this field in the center of a loop as
B(t) = μ0·I(t)/(2R)
If electric current I(t) is variable, magnetic field intensity vector B(t) is variable at all points around wire loop A, including points around wire loop B, if it's relatively close.
Therefore, the magnetic flux Φ(t) through wire loop B will be variable.
Consequently, the induced EMF
U(t) = −dΦ(t)/dt
will not be zero.
At this point it's appropriate to mention that, if wire loop A is a tight wire spiral of N loops, the variable magnetic field and, therefore, variable magnetic flux through wire loop B will be N times stronger.
That results in N times stronger EMF induced in wire loop B.
Analogously, if wire loop B is a tight wire spiral of M loops, the same EMF will be induced in each loop and, therefore, combined EMF will be M times stronger than if B consists of only a single loop.
The above considerations bring us to an idea of a transformer - a device allowing to change voltage in a circuit. This will be discussed in a separate lecture.


No comments:
Post a Comment