Solenoid: UNIZOR.COM - Physics4Teens - Electromagnetism - Magnetism of E...

Notes to a video lecture on http://www.unizor.com



Solenoid



Solenoid is a wire spiral like on this picture



It can be considered as a combination of individual circular wire loops.

We will consider an ideal case when the wire is infinitesimally thin,
the length of a solenoid along its axis is infinite and there is a
direct electric current running through it, that is running through each
of its loops.

Our purpose, as in a case of a single loop, is to determine the magnetic field inside such a solenoid.



Position our infinite in length solenoid along the X-axis such that the
X-axis is the axis of a solenoid. Let the radius of a solenoid's loops
be R and the density of the loops per unit of length along X-axis be N, that is, each, however small, segment dX on the X-axis contains N·dX loops.

Assume a direct electric current I is running through all loops.



Since a solenoid is infinite, magnetic field created by an electric
current running through it should be the same at any point on its axis.

So, let's calculate the intensity of a magnetic field B at the origin of coordinates. At any other point on the X-axis it will be the same.



The method of calculation the magnetic field is as follows.

Firstly, we will calculate the intensity of the magnetic field at
the origin of coordinates, generated by a single loop at the distance X from this point.

Secondary, we will take into account the density of the loops and
increase the calculated intensity of a single loop by a number of loops
on a segment from X to X+dX, assuming dX is infinitesimal increment.

The final step is to integrate the obtained intensity for all X from −∞ to +∞.



1. Magnetic field from a single loop at distance X from the origin of coordinates



Calculations of the magnetic field at any point on the axis going
through a wire loop is similar to but more complex than the calculation
of the magnetic field at the center of a loop we studied in the previous
lecture.

The picture below represents the general view of the wire loop with a point O,
where we want to evaluate its magnetic field and, below this general
view, the same loop as viewed from a plane this loop belongs to
perpendicularly to the X-axis.



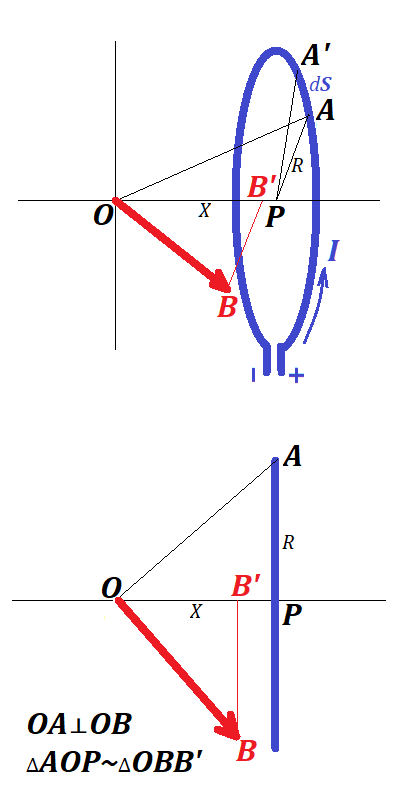
As we know, the intensity OB of the magnetic field at point O, generated by an infinitesimal segment dS of a wire loop located at point on a loop A is perpendicular to both electric current I at point A and vector AO from a point on a loop A to a point of interest - the origin of coordinates O.



The direction of the electric current at point A is perpendicular to the plane of a picture. Therefore, vector of intensity OB is within a plane of a picture, as well as line AO. Now all lines we are interested in are on the plane of a picture and vector of magnetic field intensity OB at point of interest - the origin of coordinates O is perpendicular to a line from point A on a loop to a point of interest O:

AO⊥OB.



Let B' be a projection of the endpoint of vector OB onto X-axis. From perpendicularity of AO to OB follows that ∠AOP=∠OBB' and triangles ΔAOP and ΔOBB' are similar.



As we know, the magnitude of magnetic field intensity at point O
depends on the distance from the loop segment with electric current,
the length of this segment, the magnitude of the electric current in it
and a sine of the angle between the direction of an electric current in a
segment and the line from a segment to a point of interest:



Since the direction of the electric current is perpendicular to a plane
of a picture, the angle between the direction of an electric current in a
segment and the line from a segment to a point of interest is 90°, so
its sine is equal to 1, and the formula for intensity of a magnetic
field at point O produced by a segment dS at point A on the loop is

dB = μ₀·I·dS / [4π(R²+X²]



We should take into consideration only the X-component of the vector of
magnetic field intensity because the Y-component will be canceled by the
corresponding Y-component of a vector of intensity produced by a
segment of a loop at diametrically opposite to point A location.

Let k = sin(∠OBB').

Hence,

k = sin(∠AOP) = R/√X²+R².

Then the X-component of vector OB is

dB_x = μ₀·I·dS·k / [4π(R²+X²)] =

= μ₀·I·dS·R / [4π(R²+X²)^3/2]



To get a magnitude of the magnetic field intensity at point O from an entire loop we have to integrate the above expression by S from 0 to 2πR, and the result will be

B_x= μ₀·I·2πR² / [4π(R²+X²)^3/2]

Simplifying this gives

B(X) = μ₀·I·R² / [2(R²+X²)^3/2]

Incidentally, if our loop is located at X=0, the formula above gives

B_x = μ₀·I / (2R),

that corresponds to the results presented in the previous lecture for intensity of a magnetic field at the center of a loop.



2. Magnetic field from all loops located at distance from X to X+dX from the origin of coordinates



This is a simple multiplication of the above expression for B_x by the number of loops located at distance from X to X+dX from the origin of coordinates, which is N·dX, where N is a density of the loops in a solenoid.

The result is the intensity of a magnetic field at point O produced by an infinitesimal segment of our infinitely long solenoid from X to X+dX
μ₀·I·R²·N·dX / [2(R²+X²)^3/2]



3. Finding the magnetic field at any point inside a solenoid by integrating the intensity produced by its segment from X to X+dX by X for an entire length of a solenoid from −∞ to +∞



The above expression should be integrated by X from −∞ to +∞ to get a total value of the intensity of the magnetic field produced by an entire infinitely long solenoid at point O (or any other point on its axis).

B = γ·∫_{[−∞;+∞]} dX / (R²+X²)^3/2

where

γ = μ₀·I·N·R²/2



Substitute X=x·R in the integral with dX=R·dx.

Infinite limits for X will be infinite limits for x.

Then integral will be

∫_{[−∞;+∞]} R·dx / (R²+R²·x²)^3/2 =

= (1/R²)·∫_{[−∞;+∞]} dx / (1+x²)^3/2

The value of the integral can be easily calculated.

The indefinite integral is

x/√1+x² + C

So, the value of the definite integral between infinite limits is equal to

1 − (−1) = 2.



Therefore,

B = γ·2/R² = μ₀·I·N



IMPORTANT: The intensity of a magnetic field at any point on an axis of
an infinitely long solenoid does not depend on its radius.

Textbooks usually state that the intensity calculated above is the same
at all points inside an infinitely long solenoid, not only at the points
along its axis. The justification and the proof of this are beyond the
scope of this course.