Dispersion on a Sphere and Rainbow: UNIZOR.COM - Physics4Teens - Waves -...

Notes to a video lecture on http://www.unizor.com

Dispersion through a Sphere

Let's analyze how a rainbow is developed after a rain or above waterfalls.
We will model this process with a set of parallel rays of white light (from the Sun) going through air and falling onto a transparent sphere (a water droplet).

Generally speaking, when a ray of light falls on a border between two substances (like air and water in case of a rainbow), part of light goes through the border, refracting on its way, and part is reflected by a border surface.

Let's first examine the simplest case of a white light ray from the Sun going through a spherical water droplet without reflection.


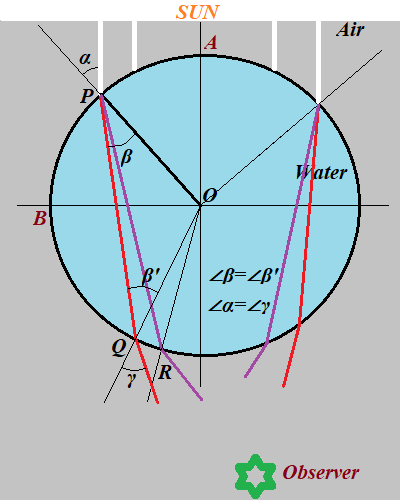
Notice that the perpendicular to a surface of a sphere at its any point is a radius to this point.

Let α be the incident angle of the white light ray coming from the air onto a transparent sphere (a water droplet hanging in the air),
β will be a refraction angle (different for different colors because of the difference in the speed of light of different wavelengths),
β' will be an incident angle, as the light goes from inside of a sphere out into the air and
γ will be a refraction angle of the light that came out from the sphere into the air.

From the Law of Refraction:
sin(α)·n_air = sin(β)·n_water
and
sin(β')·n_water = sin(γ)·n_air

Incidentally, since OP=OQ=OR, ∠β = ∠β'.
Therefore,
sin(α)·n_air = sin(γ)·n_air
from which follows that
∠α = ∠γ.

So, the white light ray is split by the refraction on two surfaces of the sphere, on entry and on exit, and we definitely have a dispersion of white light, as it goes from the air through a sphere of the water droplet and into the air again.

As mentioned before, not all the light goes along the path on the picture above. On each sphere surface, on entry into or exit from a droplet of water, the light is partially reflected. Moreover, light internally partially reflected inside a sphere can be partially reflected multiple times before it exits the sphere, each time scattering rays in different directions.

We assume that the rays of white light from the Sun are parallel and fall similarly on all the water droplets in the air.
We can also assume that immediately after the rain with high humidity in the air or above the waterfall the concentration of water droplets is significant, so that significant amount of light would hit some droplets, refract, splitting the white light into its color components, and only then will reach the eyes of an observer.

With a fixed position of the Sun in the sky and an observer on the ground, for each given droplet of water, there is only a narrow set of sun rays that go through a droplet, disperse into a conical spectrum of colors and reaches the eyes of an observer.

Moreover, if a particular component of a particular white sun ray, like red, is directed by refractions into an eye of an observer, the other component of the same white sun ray, like green, will miss this eye; it's a green component of another (neighboring) white sun ray, that is refracted by another water droplet, will reach the same eye.
That green light will fall into the eye at a different angle than the red described above, and that's why we see red light in one point of a sky and green in another, all colors in the same sequence, in order of their refractive index in water.

The refraction without internal reflection described above will produce colorful rainbow, but an observer at a position presented on the picture above might not be able to see it because the Sun will brightly shine straight into his eyes.
More practical rainbow observation can be obtained if the Sun is behind or on the side from an observer and, even better, when an observer is shielded from the direct sun rays by trees or buildings or mountains.

Consider what happens if the sun rays after penetrating the water droplet reflect from the inside of a droplet and then refract on the way out going into the eyes of an observer.


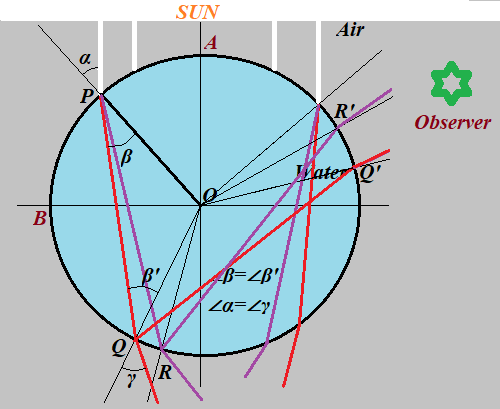
The ray of white light hits a water droplet at point P, goes through the surface of water, refracts to points from Q (for red) to R (for violet).
Then the whole spectrum of these colorful rays reflects from the inside of a water surface to points from Q' to R'.
Here the rays penetrate the surface of water and come to the air, refracting again and going to the eyes of an observer.

In this scenario the Sun does not directly flashes into the eyes of an observer, and the rays of different colors can be seen.
All other considerations about how we see different colors explained above are applicable to this case as well.

In theory, the light can be internally reflected more than once, and, correspondingly, the rainbow will be visible in more than one place on the sky.
However, we always see a circularly formed rainbow, which requires an additional explanation.
So, let's talk about why a rainbow has its circular shape.

Imagine a line from the Sun to an observer as the Z-axis of some Cartesian coordinates in space with an observer being at coordinate z=0 and the Sun at some large positive Z-coordinate.
Assume that the cloud of water droplets is in space with also positive Z-coordinates, that is the cloud is in-between an observer and the Sun along the Z-axis.
If a particular component, like red, of a refracted white sun ray from the water droplet with coordinates (x,y,z) reaches the eye of an observer, then there will be the same color component, refracted into the eye of an observer by another droplet that is positioned at the same angle to an observer from the Z-axis and at the same distance from the Z-axis, as represented on this picture:

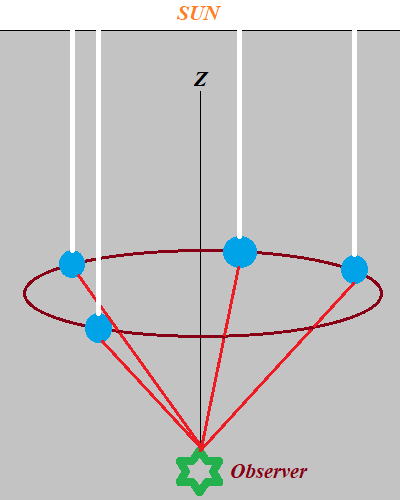
That makes all the places, where an observer sees red light, a circle in the sky.
If the Sun is not in the zenith, but positioned closer to a horizon, the circle will not be complete. Also, if water droplets do not fill an entire sky, the rainbow would not be a complete circle either.
But, some partial circle of a rainbow will be observed in the sky.

The above case is not very pactical, as the Sun flashes right in the eyes of an observer, preventing to see the rainbow.
In a more practical case, when the cloud of water droplets is not between an observer and the Sun along the Z-axis. Instead, an observer is in-between a cloud of water droplets and the Sun.

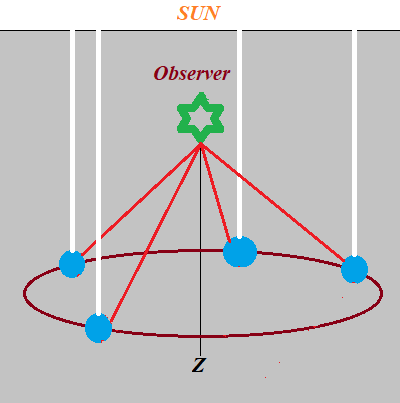
As we mentioned before, the sun rays are always partially go through a surface of the water and partially reflected. This reflection can be observed on the outside of a water droplet and inside it (internal reflection).

As the Sun sends its white light rays towards a cloud of water droplets in front of an observer from behind his back, some rays go through a surface of water droplets, refracting on the way, then they reflect back against the opposite inner surface of a droplet, go through another surface, refracting again, and into the eye of an observer.
This is how a rainbow is formed when the Sun is behind the back of an observer, as he looks at the water droplets in the sky.
Again, the same circular formation of the places in the sky that have the same color can be observed because of the same considerations as above.

Continuing this train of thought and taking into consideration the effect of partial reflection of light, the same ray of sunlight can produce one color component by going through two surfaces of a droplet, then, after partial reflection from the inside of a droplet and subsequent refraction, another color ray is produced directed differently then the first one.
That's why sometimes we see double rainbow concentric to the first one, but weaker in intensity.