Dispersion - Prism: UNIZOR.COM - Physics4Teens - Waves - Phenomena of Light

Notes to a video lecture on http://www.unizor.com

Dispersion through a Prism

Let's analyze now what happens with the ray of white light going through a side of a regular right triangular prism (with equilateral triangle as each base) on a trajectory parallel to prism's bases, as represented in a prism's section along a trajectory of this ray on the picture below.


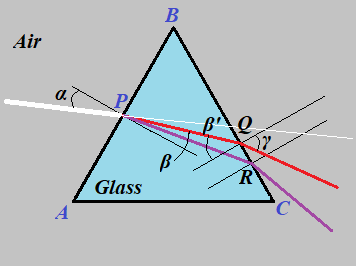
Let α be the incident angle of the white light ray coming from the air onto a side surface of a prism parallel to the bases, hitting it at point P on the line AB of the prism section ΔABC.

Let β be the angle of refraction after this ray passed the border surface between the air and the glass. We will consider the fastest visible light in the glass, red, and its value of β_r separately from the slowest color, violet, and its value of β_v, while values of the refraction angle for other colors to be in between these two extremes.

Then, β' will be the group name for incident angles, when the rays of different colors reach the other side of a prism BC. We will differentiate points Q, where the red component of the ray of white light hits the side of a prism, and R, where the violet component hits the prism's side and distinguish β'_r for red ray of light from β'_v for violet one.

Finally, γ is a group name for refraction angles of red (γ_r) or violet (γ_v) rays after they pass the border from the glass into the air.

The Law of Refraction allows to calculate the refraction angles β_r and β_v, based on the incident angle α and refractive indices n_r and n_v of glass for each color, as described in the previous lecture:
sin(β_i) = sin(α)·n_i /n_air
where we can safely assume that n_air=1 for all colors and i index is either r for red or v for violet.

Since the light goes from the substance with a smaller refractive index (air) into a substance with a larger refractive index (glass), the refraction angle will be smaller than that of incident.

Simple geometry of ΔABC allows to calculate the angle of incident β' of the ray, as it goes from inside the prism out to the air through the side BC of a prism, based on the value of the angle β:
∠BPQ = 90° − β
∠PBQ = 60°
∠BQP = 180° − ∠BQP −
− ∠PBQ = 30° + β
β' = 90° − ∠BQP = 60° − β

Using the same Law of Refraction and knowing the incident angle of rays β', as they come out from the glass into the air, we can calculate the refraction angle γ for each color using the derived above formula
sin(β'_i)·n_i = sin(γ_i)·n_air
sin(γ_i) = sin(β'_i)·n_i /n_air
where we can safely assume that n_air=1 for all colors and i index is either r for red or v for violet.

In the previous lecture we have calculated the values for different refraction angles β with the angle of incident α=30°.

Color	α	n	β
Red	30°	1.520	19.205°
Orange	30°	1.522	19.179°
Yellow	30°	1.523	19.166°
Green	30°	1.526	19.126°
Blue	30°	1.531	19.062°
Violet	30°	1.538	18.971°

Now, using these values of β and values of β'=60°−β, we can continue with calculating the final refraction angle γ.
Notice, the refraction angle γ will always be larger than incident angle β' because the ray of light goes from a substance with a higher refractive index (glass) into a substance with the lower one.

Another very interesting phenomenon can be observed in this case. The refraction angles for blue and violet colors cannot be calculated, because the sine of the refraction angle, as calculated based on the incident angle, refractive index of the glass and the Law of Refraction, becomes greater than 1. It indicates that rays, if falling at a sufficiently large incident angle from within a glass, will not go out, but will be internally reflected from the wall of the prism.
This phenomenon is called the total internal reflection and is the basis for fiber optics, where light signals are sent along a thin tube made of glass or similar material, so they internally reflected off the walls and propagate only inside the tube.

Here are the final results of the calculation of refraction angles on exit from the prism for different colors.

Color	β' = = 60°−β	n	γ
Red	40.795°	1.520	83.3°
Orange	40.821°	1.522	84.2°
Yellow	40.834°	1.523	84.8°
Green	40.874°	1.526	87.0°
Blue	40.938°	1.531	none
Violet	41.029°	1.538	none

Let's analyze the angular deviation of the final rays of light after leaving the prism from the original direction of the white light.
The final angular deviation can be represented as a sum of two: the angular deviation on the border from air to glass and the angular deviation on the border from glass to air.
The first one is
Δ₁ = α − β
The second one is
Δ₂ = γ − β'
Since β'=60°−β, the final formula for total deviation Δ is
Δ = α − β + γ − β' =
= α − β + γ − 60° + β =
= α + γ − 60°

In our example of the original incident angle α=30° and taking into account average refractive index of glass for yellow color, the refraction angle γ=84.8°. This gives the deviation total to be
Δ=30°+84.8°−60=54.8°
Obviously, it's a little smaller for lights faster than yellow, like red or orange, and a little larger for lights slower than yellow, like green, but still the values are pretty close to this average one.