Water Depth Problem
If we look at some object at the bottom of a water from above, it looks closer than it really is.
Why?
Consider the process of measuring a distance to an object by looking at it. We feel that the object is closer, if we have to move the pupils of our eyes closer to each other pointing to an object using muscles that move our eyes. Another group of muscles make the lenses of our eyes more curved to focus the image on the retina at the back of the eyes, where optic nerves are ending.
The intensity with which our muscles work to focus on an object is somehow translated in the brain into a feeling of the distance the object is located at. Greater intensity of eye muscles contraction corresponds to a shorter distance to an object of interest.
Consider now what happens when we look at some object on the bottom of the water from above the water viewpoint.
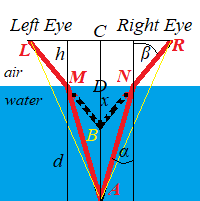
Our eyes see an object, when the light is emitted by or reflected from it.
Let some object be at the bottom of the water at location A, as presented on the picture above.
Taking into consideration refraction of light from the object, when it crosses the border from water to air, we conclude that the rays of light from an object directed straight into our eyes will not reach the eyes along the yellow lines AL and AR, but will be refracted to the sides.
Instead, red rays AM and AN, correspondingly, refracted at the border between air and water, continue their path along lines ML and NR and reach our eyes.
Point B, an intersection of lines LM and RN, will be a perceived location of an object.
Obviously, the angle of vision ∠LBR is greater than ∠LAR and, therefore, it requires a greater strain on the eyes' muscles to focus on the image of an object, which entails our perception of an object to be at location B, which is closer to us than it really is at location A.
Let's do some calculations based on the laws of refraction that we know.
Assume, the depth of the water is AD=d and we are at the height CD=h above the water.
Also important is the distance between our eyes, which we will set to LR=s.
The real distance from our face to an object at the bottom of the pool is along the perpendicular AC from point A to line LR connecting the eyes and is equal to d+h.
Let's calculate the perceived distance, which is a distance from point B to line LR along the perpendicular BC.
Let's introduced the following variables of our problem:
incident angle α=∠MAD,
refraction angle β=∠MBD,
distance x=BD.
Now we will construct three equations with these unknown variables.
From triangle ΔBCL:
LC/BC = tan(∠LBC).
Therefore,
s/2 = (x+h)·tan(β)
This is our first equation.
From triangle ΔADM:
MD/AD = tan(∠MAD).
Therefore,
s/2 = h·tan(β) + d·tan(α)
This is our second equation.
The third equation is the Law of Refraction, assuming the refraction indices of air nair and water nwater are known:
nwater·sin(α) = nair·sin(β)
Subtracting the first equation from the second, we get
0 = (x+h)·tan(β) −
− [h·tan(β) + d·tan(α)]
from which follows
x/d = tan(α)/tan(β)
At this time most physicists assume that the angles of incidents and refraction are small enough and just approximate the ratio of tangents with the ratio of sinuses (known from the Law of Refraction) and conclude that
x/d ≅ sin(α)/sin(β) =
= nair/nwater
Precise expression requires more involved calculations and we leave them to interested students to come up with an exact solution.
Indices of refraction for air and water are:
nair ≅ 1.0003
nwater ≅ 1.333
Therefore, the ratio above that evaluates the visible decrease in depth of water is
nair/nwater ≅ 0.75
So, the perceived depth of the water is smaller than the real one, approximately, by the factor nair/nwater ≅ 0.75.


No comments:
Post a Comment