Galilean NON-Invariance
Clouds on the Horizon
At the end of the 19th century physicists were generally of a positive opinion about the state of Physics.
Newton's mechanics and theory of gravitation, Coulomb's laws of electrostatic were pretty much in good shape.
The properties of electromagnetic field were well described by Maxwell equations.
The theory of aether as a medium for electromagnetic waves, while not being absolutely satisfactory for physicists, was the only one available to explain the observable wave character of light and its constant speed that depends only on medium's characteristics of electric permittivity and magnetic permeability.
All was not bad... except a couple of "small" things.
First, the experiment of Michelson-Morley in 1887 attempted to detect aether and showed negative result, as was confirmed by many other experiments afterwards.
The aether was supposed to have too many contradictory properties to satisfy all the experimental data, and physicists became more and more skeptical about this theory.
Second, the Newtonian laws of mechanics an gravitation, as well as Coulomb's law of electrostatics showed the invariance relative to Galilean transformation of coordinates between two inertial frames, but the laws related to electromagnetism and, in particular, Lorentz force and Maxwell equations showed that these laws and equations are not invariant, if we use Galilean transformations.
Their expression in one inertial reference frame, transformed into another frame using the Galilean transformation, took a different form than in the original frame.
An important details about the laws that are invariant relative to Galilean transformation is that they are dependent either on a distance between two points, like in case of gravity or electrostatic forces, which is invariant under Galilean transformation as demonstrated in the lecture Metric Invariance of this chapter, or on acceleration, like in case of Newton's laws of mechanics, which is the second derivative of the coordinates as linear functions of time in Galilean transformation, and the second derivative nullifies the dependency on the velocity of one reference frame relative to another.
At the same time, electromagnetic properties and forces depend on the velocity of charged objects (Lorentz force), which is the first derivative of coordinates by time, and the first derivative leaves the velocity as a participant in the equations, thus making the laws non-invariant to Galilean transformation.
Indeed,
if x=X−v·t/
then dx/dt=dX/dt−v,
which shows clear dependency on velocity of a moving frame relatively to a stationary, and velocity participates in Maxwell equations.
Aether as Light Medium
Wave properties of light were known and well accepted by physicists at the end of 19th century.
It was also assumed that light waves need a medium to carry them analogously to sound waves that need a medium, like air, to propagate.
The medium that carries light was called aether (or ether).
A consequence from Maxwell equations was that the waves of light have a fixed speed of propagation that depends only on the medium's electromagnetic properties, the electric permittivity ε and magnetic permeability μ.
But, if the aether is a physical substance, its movement relative to the source of light should affect the speed of light propagation similarly to air wind affecting the propagation of sound waves, which are faster along the direction of a wind and slower against it.
Many experiments intended towards detection some difference in light propagation related to movement of the Earth through aether ended up with negative results. For some of them physicists came up with explanations why the results were negative, but others were just hanging as unexplainable in the framework of the aether theory.
The most famous experiment to detect aether wind was that of Michelson and Morley in 1887.
If aether exists and our planet is moving in it like a submarine in the ocean, the light should have different speed if measured along two perpendicular to each other directions.
The experiment convincingly showed that there is no difference in the speed of light.
Magnetism of Electric Current
The following thought experiment demonstrates that from the pre-relativistic viewpoint, when space and time are understood in absolute classic Galilean sense, the behavior of a moving charge in constant uniform electromagnetic field depends on the reference frame from which it is observed.
This contradicts the Relativity Principle, which is considered one of the major cornerstones of Physics.
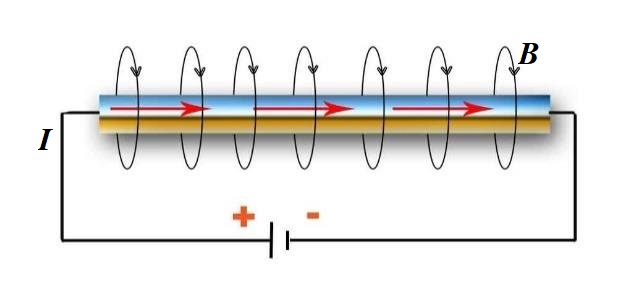
Consider an electrically neutral straight line wire in a vacuum. Since it's electrically neutral, there is no electrostatic field around it and the number of electrons equals to the number of protons.
Let's connect it to a battery; electric current will start running, and electrons will start moving in one direction, consumed by the positive pole of a battery and emitted from its negative pole.
During this process the number of electrons consumed by a positive pole per unit of time will be equal to the number of electrons emitted from the negative pole, which preserves the electrostatic neutrality of a wire as a whole.
Therefore, there is no electrostatic field around the wire.
As we know, there is a magnetic field around an electric current produced by moving electrons inside a wire. Its field lines form circles around a wire. This field does not change in time, as long as the battery maintains the constant voltage and the electric current is not changed, all its characteristics are constant.
The formula describing this magnetic field (to refresh your knowledge, see Magnetism of Electric Current in the Electromagnetism part of Physics 4 Teens course on UNIZOR.COM) is
B = μ0·I/(2πR)
where
B - intensity of a magnetic field (in tesla)
μ0 - permeability of vacuum (constant characteristic of vacuum)
I - constant electric current
R - distance from a wire to a point where magnetic field intensity is measured.
As we see from this formula, at any given point around this wire the intensity of the magnetic field is constant.
Assume that at some distance from a wire a positively charged particle starts moving on a parallel to a wire trajectory in the same direction and the same speed as electrons inside a wire.
This particle moves along a trajectory that perpendicularly intersects magnetic field lines around a wire and, therefore, will experience the Lorentz force that is directed perpendicularly to its velocity and to magnetic field lines.
In vector form this force is
F = q·v⨯B
where
F - force acting on a particle
(in newtons N)
q - particle's charge
(in coulomb C)
v - linear speed of a particle
(in meters per second m/s)
B - intensity of a magnetic field
(in tesla T)
This Lorentz force will cause a particle to deviate from the straight line parallel to a wire and the distance from this particle to a wire will change.
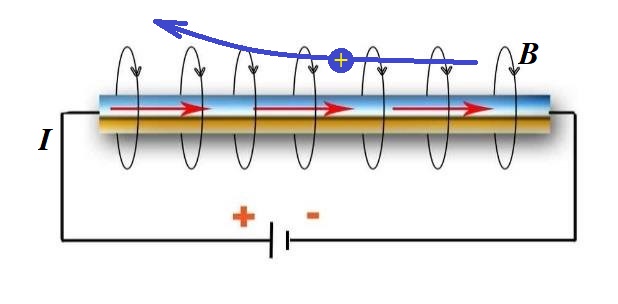
Consider now the same arrangement from the point of view of an observer traveling with our particle.
In this reference frame a particle and electrons in the wire are standing still, since our observer moves in the same direction and with the same speed as they are.
Instead, our observer sees protons moving in the opposite direction than electrons in the previous case. That means that we still have the same electric current in the wire, the same magnetic field is produced by this electric current, and it has the same circular magnetic field lines.
The magnetic field seems the same, but a particle now is not moving in this reference frame, is NOT crossing magnetic field lines, which means there is no Lorentz force and the distance between a particle and a wire remains constant.
So, it looks like the laws of nature are different, if observed from two different inertial frames. In the first reference frame the particle's distance from the wire was changing as the time goes, while in the second reference frame the particle was at the same distance from a wire all the time. This contradicts the Principle of Relativity generally accepted as universal.
Maxwell Equations and Galilean Transformation
As it turns out, some Maxwell Equations ARE NOT INVARIANT relative to Galilean Transformation.
Without going into mathematical details of actually proving this non-invariance, it can be seen from the previous qualitative analysis of an electrically charged particle moving along a wire with electric current viewed from two inertial reference frames described above.
In one reference frame there is a Lorentz force acting on this particle, causing its deviation from a straight line trajectory and changing its distance from a wire, while in another reference frame there is no such force, a particle continues its movement along a trajectory parallel to a wire, preserving the distance between a particle and a wire.
This contradicts the Relativity Principle.


No comments:
Post a Comment