Moving Charge - Problem 3
This problem is based on previous lectures about magnetic field around a straight wire with electric current running through it and the one generated by a moving electrically charged particle.
We would like to establish a connection between two formulas:
(a) the formula for a magnitude of a magnetic field intensity vector of a long straight wire with electric current running through it
B = μ·I/(2πR)
where
B is an intensity of a magnetic field at observation point
μ is permeability of media around a wire
I is an electric current running through a wire
R is a shortest distance of an observer from a wire
(all constants)
and
(b) the formula for a magnitude of a magnetic field intensity vector of the moving electrically charged particle
B = μ·q·v·sin(φ)/(4πr²)
where
B(t) is a variable intensity of a magnetic field at observation point
μ is permeability of media between a particle and an observer
q is an electric charge of a particle
v is a particle's speed
φ(t) is a variable angle between the direction of a movement of a particle and direction from an observer to a particle.
r(t) is a variable distance of an observer from a particle
(notice that φ, r and, therefore, B are variable in this case)
The problem is to derive formula (a) from formula (b) considering an electric current inside a wire of formula (a) as a flow of particles of formula (b).
We compare only expressions for magnitudes, as the direction of magnetic field intensity vectors is, obviously, the same - perpendicularly to both trajectory of electric charges and direction from an observer to a wire or to a moving particle.
Solution
To bring analytics and math to our problem, we assume that each infinitesimal part of a wire with electric current running through it is a moving electrically charged particle.
We will examine the magnetic field generated by this moving electrically charged particle and integrate all the individual magnetic field intensities generated by all such particles along an infinite wire.
We intentionally did not use the vector expression of magnetic field intensity with a vector product of velocity vector of a particle and a unit vector from an observer to a particle v⨯u. As we stated, the direction of magnetic intensity vector in both cases (a) and (b) is, obviously, the same. So, using v·sin(φ) as a magnitude of vector v⨯u simplifies the problem.
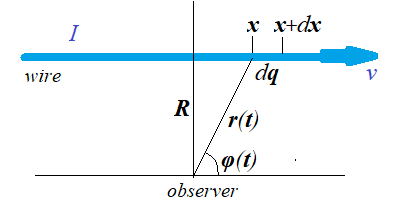
The most important part of a solution is to represent an electric current I as an infinite set of infinitesimal particles carrying infinitesimal electric charge and moving along a wire with constant speed.
Electric current inside a wire consists of electrons moving in some direction. Ideally, they all move with a uniform and constant speed v.
Assume, a linear density of electrons inside a wire is δ(coulomb per meter C/m).
Wire is infinite, so let's take some point on it as a zero coordinate and consider a piece of wire from coordinate x to x+dx.
This linear piece of wire of the length dx(m) contains dq=δ·dx(C) of electric charge.
Moving with speed v(m/s), this small charge will cover a distance from x to x+dx during the time dt=dx/v.
Charge dq moving along a wire during time dt constitute an electric current I=dq/dt.
Therefore,
I = dq/dt = (δ·dx)/(dx/v) = δ·v
Using this expression for electric current, formula (a) would be equivalent to
(aa) B = μ·δ·v/(2πR)
We will prove that formula (b) for a magnetic field of a moving particle will lead to the above formula (aa), if a current in a wire is viewed as a set of particles moving along a wire.
Let's use the formula (b) to calculate the intensity of a magnetic field generated by a particle carrying infinitesimal charge dq at position x of a wire and moving along a wire with speed v.
dB = μ·dq·v·sin(φ)/(4πr²)
Here we can replace r with √R²+x².
Charge dq can be replaced with δ·dx.
Also we can replace sin(φ) with R/√R²+x².
Now the expression for infinitesimal magnetic field intensity generated by infinitesimal charge dq moving with speed v is as follows
dB = μ·δ·dx·v·R/[4π(R²+x²)3/2]
Integrating this expression by x from −∞ to +∞ produce the total impact of magnetic field intensity produced by an entire wire. It should be the same as in formula (aa). If it does, it would be an additional proof that Physics does not have inner contradictions in its laws.
Let's check it out.
First of all, both expressions, (aa) for a magnetic field of an entire wire and the above expression for a field produced by a charge dq, contain constant multipliers μ (permeability of media), δ (linear density of electric charge) and v (speed of particles inside a wire). They will, obviously cancel each other.
So, all we have to prove is that the integration of
dx·R/[4π(R²+x²)3/2]
along all values of x (positive and negative) results in 1/(2πR).
More simplifications can be obtained by considering that integration of an even function from −∞ to +∞ is equivalent to integration from 0 to +∞ times 2.
So, we have to prove that
2·∫[0,+∞]dx·R/[4π(R²+x²)3/2]
is equal to 1/(2πR).
Also, by multiplying both formula by 2πR, our task is reduced to proving that
∫[0,+∞]dx·R²/[(R²+x²)3/2] = 1
The last simplification is to substitute
y = x/R
x = y·R
dx = dy·R
Limits of integration from 0 to +∞ remain the same in this substitution.
The result is to prove that
∫[0,+∞]dy·R³/[(R²+y²·R²)3/2] = 1
Here R is, obviously, cancels out, and the only thing to prove is that
∫[0,+∞]dy/[(1+y²)3/2] = 1
To calculate the above integral, let's use the substitution
y = tan(z)
dy = dz/cos²(z)
The limits of integration for y from zero to +∞ will change from zero to π/2 for z.
Now our integral looks like
∫[0,π/2]dz/[cos²(z)·(1+tan²(z))3/2]
Since 1+tan²(z)=1/cos²(z), our integral equals to
∫[0,π/2]dz·cos(z) = sin(z)|[0,π/2] =
= sin(π/2)−sin(0) = 1
As we see, the equality has been proven.
That means that two different formulas mentioned above, (a) for a magnetic field of an electric current and (b) for a magnetic field of a moving charge, are completely in agreement with each other.


No comments:
Post a Comment