Time Measuring
We are planning to conduct a few thought experiments. For this we need some simple clock to measure time between events in different inertial reference frames.
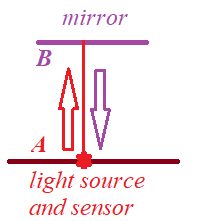
Consider the following clock construction.
Take a rigid rod, its edges are points A and B.
At edge point A we install the source of light and a sensor of light.
At edge point B we install a mirror that reflects a beam of light back to its origin.
We define the unit of time as the time from a moment we send a beam of light from point A to point B till we receive back a reflected beam back at point A.
This will be our light clock that we can use to measure any time interval.
As confirmed by numerous experiments and follows from the Maxwell equations, the speed of light c is exactly the same in any inertial reference frame in empty space.
That's what makes this clock perfect for time measurement.
According to the Principle of Relativity, which we accept as an axiom, any observer in one inertial reference frame, who measured a unit of time by this light clock, can go to another inertial reference frame, take this clock with him, and the interval of time measured by this clock there would be exactly the same.
If some process, like boiling a pot of water or growing corn, in one inertial frame takes certain time, according to this light clock, exactly the same process would take exactly the same amount of time in any other inertial reference frame using the same clock locally to that frame.
Now consider two inertial reference frames:
frame α with Cartesian coordinates X, Y, Z and time T
and frame β with Cartesian coordinates x, y, z and time t.
So, all capital coordinates (X, Y, Z) and time (T) will be related to α-frame, events occurring in it (α-events) and observer at rest in it (α-observer).
Similarly, all lower case coordinates (x, y, z) and time (t) will be related to β-frame, events occurring in it (β-events) and observer at rest in it (β-observer).
Assume that at time T=t=0 both frames coincide, that is their origins are at the same point in space and their axes overlap, but frame β is moving relative to α along the X-axis with speed v, so the velocity vector of β-frame in α-frame coordinates has components {v,0,0}.
Since the movement is relative, we can say at the same time that frame α is moving relative to β along the X-axis with speed −v, so the velocity vector of α-frame in β-frame coordinates has components {−v,0,0}.
Consider identical light clocks in both α- and β-frames arranged between local in each frame points A{0,0,0} and B{0,0,R}, where R is any real number. The first point is an origin of a corresponding frame and the second point is on the Z-axis on a distance R from the origin.
Since the distance between these points in each frame is R, the interval of time between emitting a ray of light from the origin and receiving a reflected ray back at the origin (with the total distance covered by light ray equaled to 2R and the speed of light c) equals in each frame for a local observer at rest in each corresponding frame to
Tα = tβ = 2R/c
Besides this local observation from within each frame, consider how the same time interval is evaluated by an observer in the other reference frame.
The interval of time for a ray of light covering in α-frame the distance from the origin of coordinates to a mirror and back can be analyzed by an observer at rest in β-frame (tα) and an interval of time for a ray of light moving in β-frame along the analogous path can be analyzed by an observer at rest in α-frame (Tβ).
These remote observations are not necessarily produce the same measurements of time interval as observed locally.
Let's see now how an observer in α-frame {X,Y,Z,T} evaluates the time interval of a round trip of a ray of light in the β-frame {x,y,z,t} moving with speed v along α's X-axis.
Assume, at some moment, when β's origin is at α coordinate {X0,0,0}, the light was emitted by the β light clock from its origin.
From a β-observer viewpoint the ray emitted by a light clock from β point {0,0,0} goes vertically along its Z-axis, reaches the point {0,0,R}, is reflected back and received at the β's origin after tβ=2R/c interval of time.
However, an observer at α who analyses the events in β-frame thinks differently.
Since β-frame is moving relatively to α-frame, from an α-observer viewpoint the ray that should reach the mirror in β-frame and reflect back should go along trajectory as on the following picture
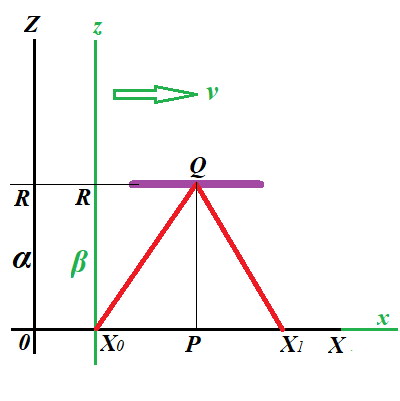
The α-observer concludes that, while the ray moves from β's origin at point X0 in α-frame coordinates towards the mirror Q, the mirror moves further to the right in α-frame with speed v, and, while the reflected ray moves back to the β's origin, this origin moves even more to the right to point X1 in α-frame coordinates.
Let's calculate the time Tβ that should pass on α-observer's clock during the time the ray in β-frame moves to a mirror and back (index β signifies the frame where an event takes place, in this case we are talking about β-event).
The distance from X0 to X1 is the distance β-frame moves during time Tβ on α-observer's clock with uniform speed v.
During the same time Tβ the light with uniform speed c covers the distance from β-frame's origin at point X0 in α-frame up to the mirror at point Q and back to β-frame's origin that by that time has moved with uniform speed v to point X1 in α-frame.
Therefore,
X0X1 = v·Tβ
X0Q + QX1 = c·Tβ
PQ = R
X0P = PX1 = ½·v·Tβ
X0Q = QX1 = ½·c·Tβ
R² + (½·v·Tβ)² = (½·c·Tβ)²
4R² = −(v·Tβ)² + (c·Tβ)²
But the β-observer's clock would show that this same process took tβ local time, which is the time light covers the distance from point β{0,0,0} straight up to point β{0,0,R} and back, covering the distance of 2R with speed c.
Therefore,
2R = c·tβ
Comparing the above expressions, we come with the following
4R² = −(v·Tβ)² + (c·Tβ)² =
= (c·tβ)²
From this we can derive the relationship between time measurement Tβ of a β-event in α-frame by a remote α-observer and time measurement tβ of the same β-event in β-frame by local β-observer.
−(v·Tβ)² + (c·Tβ)² = (c·tβ)²
From this follows
(1−(v²/c²))·Tβ² = tβ²
Traditionally, physicists use symbol γ to express this relationships between the timing in both reference frames
γ = 1/√1−(v²/c²)
Then the above relationship takes the form of
Tβ = γ·tβ
As you see, a remote evaluation of a time interval of an event is always greater than local.
This property of time is symmetrical.
The α-event takes longer, if evaluated from the β-frame than locally in the α-frame.
tα = γ·Tα
In some way it's similar to a situation when two people look at each other from a distance. Each person sees the other smaller than that person really is.
This relationship between measuring a time interval of certain event by a local observer in some inertial frame and the time of the same event measured by an observer in another inertial frame moving relative to the first one is called time dilation.
TIME IS NOT ABSOLUTE


No comments:
Post a Comment