Magnetism of
Moving Charged Particle
In the previous lecture, using some common sense consideration and logic supported by experiments, we came up with an expression for a magnetic field around a straight line wire with electric current running through it
B = μ0I/(2πR)
where
I is an electric current running through a wire in ampere (A),
R is a distance from a wire with an electric current in meter (m),
B is an intensity of a magnetic field in tesla (T),
μ0 is the permeability of free space in newtons per ampere squared (N/A²)
Let's use similar logic to evaluate an intensity of a magnetic field generated by a single moving electrically charged particle.
Assume, an electrically charged particle carrying charge q coulombs (C) is uniformly moving in vacuum along a straight line trajectory r(t) with constant velocity vector
v = dr(t)/dt
Assume further that an observer is located at the origin of coordinates O, and his task is to measure the intensity of a magnetic field created by this moving particle.
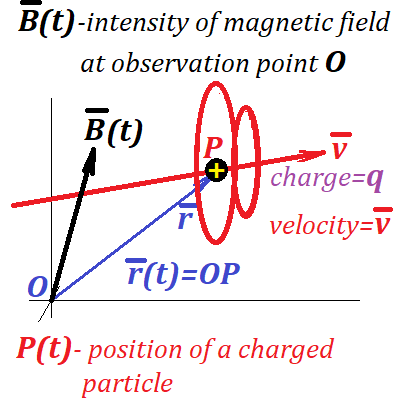
Since a charged particle is moving, it creates a magnetic field around it.
The force lines of this magnetic field form circles around a straight line trajectory of a particle. Each circle lies in the plane perpendicular to a trajectory and centered on a point of this trajectory.
Vectors of magnetic field forces (intensity vectors B(t,x,y,z)) at any point in space around a moving particle will be tangent to these circles.
The magnitude of the intensity of a magnetic field depends on certain parameters. The following statements about this magnitude are theoretically sound and confirmed by experiments.
This magnitude should be
(a) proportional to an amount of charge q carried by a particle,
(b) proportional to a particle's speed v,
(c) inversely proportional to a square of a distance r from a moving particle,
(d) depends on the angle between a particle's velocity vector v and a direction from an observer to a moving particle r(t) that we will describe for now as ∠(r(t),v).
The dependency (a) and (b) are obvious and need no explanation.
Inverse square rule (c) occurs everywhere in other fields (gravitational as Newton's Law, electrostatic as Coulomb's Law).
We usually put 4πr² into denominator of expressions for a force, where r is a distance from the source of this force.
The reason for this is that the energy emitted by this source is evenly distributed in our three-dimensional world in all directions and, when it reaches an observer on a distance r, actually falls on a whole sphere of a radius r around the source with an area of this sphere, as we know, 4πr².
The dependence (d) of the magnetic field intensity on the angle between a particle's velocity vector and a direction from an observer to a moving particle needs more explanation and analysis.
Consider two cases presented on pictures below.
Here we present only two dimensions to make the explanation more obvious.
An observer is measuring the intensity of a magnetic field by analyzing a density of an amount of magnetic energy falling on some measuring gadget.
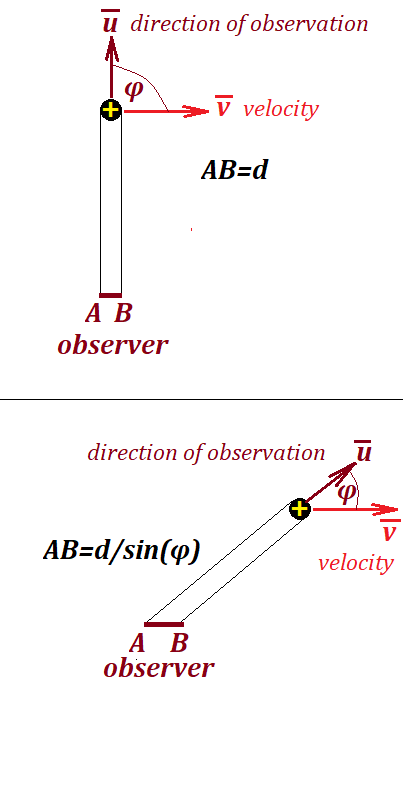
In both cases the distance from a source of magnetic field (a moving charge) to an observer in the same.
In the first case the observation line denoted by a unit vector u is perpendicular to a velocity vector v of a particle. In the second case there is an acute angle between these two vectors.
The amount of energy emitted by a source (the proper term is magnetic field flux) in the first case and falling on a segment AB is the same as an amount of energy falling on a longer segment AB in the second case, and the length of this segment AB is longer by a factor 1/sin(φ) than in the first case.
Therefore, the observed density of magnetic field flux, which we call field intensity, must be less in the second case than in the first by a factor sin(φ).
This situation is exactly analogous to an amount of heat per unit of area (heat density) from the sun, when it shines perpendicularly to the Earth surface around noon, and at some later (or earlier) time, when the sun is not in zenith. The heat density is at maximum, when the sun shines straight down onto Earth surface and is less in the morning or evening, when the sun is closer to horizon and shines at other than the right angle.
All the above considerations lead us to the following formula for a magnitude of magnetic field intensity B
B ∝ q·v·sin(φ)/(4πr²)
We can transform this formula to incorporate the direction of the vector of magnetic field intensity. It's supposed to be tangent to a circle that lies in the plane perpendicular to a particle's velocity, centered on this trajectory and goes through a point of observation.
All these considerations lead us to the following expression for intensity of a magnetic field
B ∝ q·v⨯u/(4πr²)
The usage of a vector product of a particle's velocity v and a unit vector in the direction of observation u assures correct representation of both direction and magnitude of the vector of magnetic field intensity.
Sometimes, to avoid using a unit vector u, it's replaced with r/r, where r is a vector from an observation point to a moving particle and r is its magnitude.
If an observation point is at the origin of Cartesian coordinates, vector r(t) describes the position of an particle as a function of time.
The first derivative of this vector by time is a velocity vector v(t)=dr(t)/dt=r'(t)
Now the magnetic field intensity of a charged particle whose position is described by a vector r(t) at the observation point at the origin of coordinates can be expressed as
B(t) ∝ q·r'(t)⨯r(t)/(4πr³(t))
Experiments show that the coefficient of proportionality in this formula is the same media permeability μ introduced in the previous lecture (μ0 in case of vacuum).
The final formula is
B(t) = μ·q·r'(t)⨯r(t)/(4πr³(t))


No comments:
Post a Comment