Polarization: UNIZOR.COM - Physics4Teens - Waves - Phenomena of Light

Notes to a video lecture on http://www.unizor.com

Polarization of Light

The light is transversal electromagnetic waves.
Each individual ray of light has electric and magnetic components, oscillating perpendicularly to each other, each within its plane.

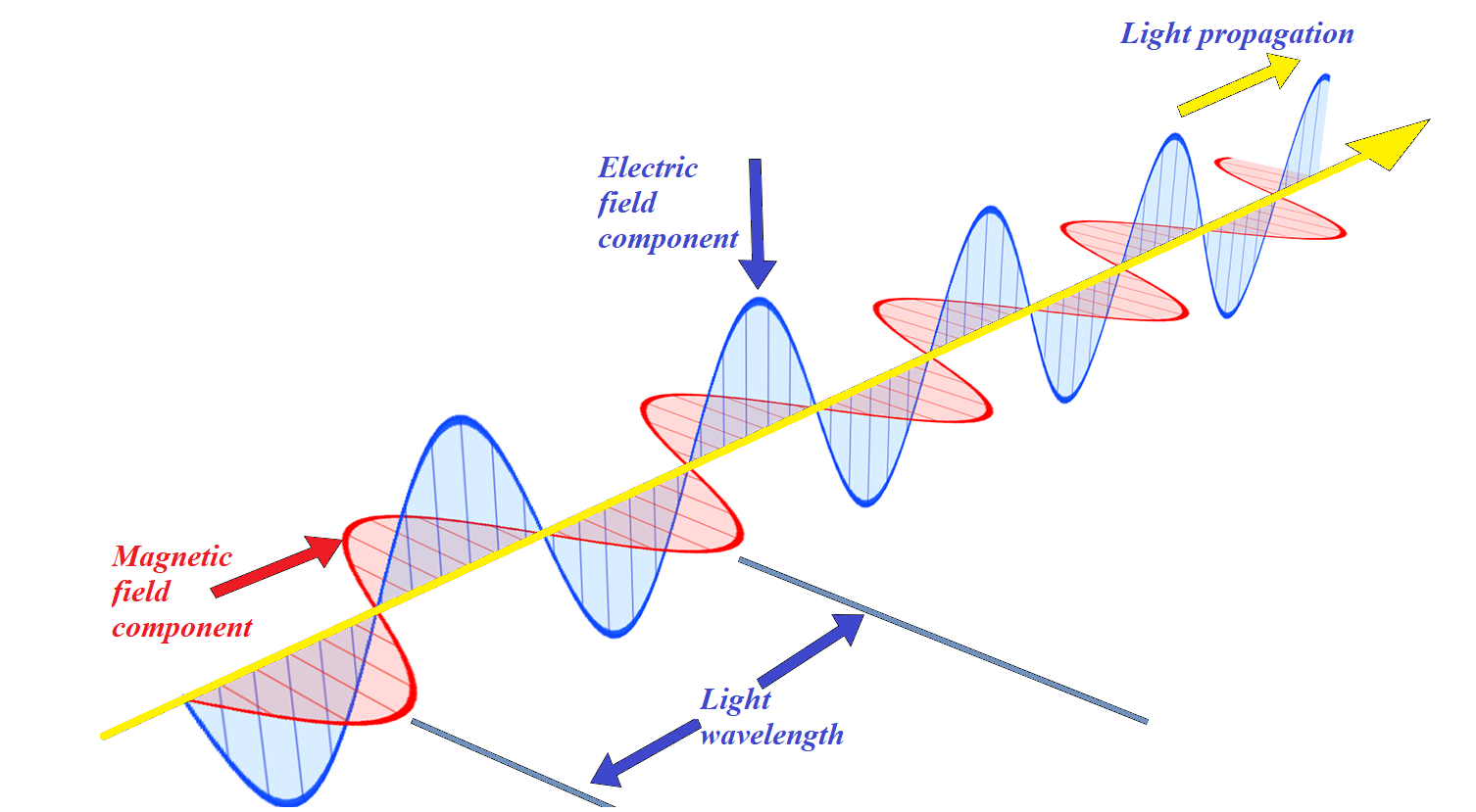
(click the right button to open a larger image in a new tab)

The light from the Sun, from a lamp and from many other sources of electromagnetic waves constitute a mix of oscillations of electric and magnetic components in all directions perpendicular to the direction of light propagation, with different amplitudes and phases.

There are some substances, called polaroids, naturally occurring crystals or artificially created, that, when placed on the trajectory of the light ray, selectively allow to pass through only oscillations in one particular plane.
This process of selecting only one particular plane of oscillations of electromagnetic waves to go through, while suppressing all others is polarization of light.

The following picture shows this process of polarization, where for simplicity only electric component is shown:

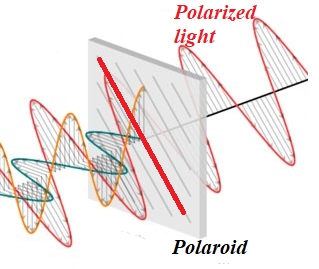
As we see, while the light rays before the polaroid consist of oscillations in all different planes, there is only one plane of polarization, where oscillations of electric component of an electromagnetic field occur after the process of polarization.

Those oscillations before a polaroid, that are already in the plane of polarization, are going through a polaroid without change.
Oscillations in a plane perpendicular to a plane of polarization are not going through at all.
All other oscillations are weakened by the polarization for the following reason.

Assume, the plane of oscillations of electric component vector E of the electromagnetic wave is at angle θ relative to a plane of polarization of a polaroid.
We can then represent vector E as a sum of two vectors, one coinciding with a plane of polarization E_in, which the polaroid let through, and another perpendicular to it E_out, which will not go through a polaroid:
E = E_in + E_out =
= E·cos(θ) + E·sin(θ)

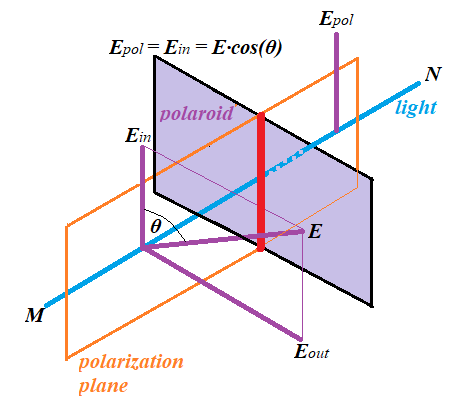
The oscillations represented by electric component E_in=E·cos(θ) coinciding with the plane of polarization will go through the polaroid and on the other side the light would be represented only by polarized
E_pol = E_in = E·cos(θ).

The brightness of the light will diminish after the polarization because almost all components of the incoming rays of light, having different amplitudes, phases and angles to a plane of polarization, will fall onto polaroid not within its plane of polarization, and only part of these rays would go through after their amplitude is multiplied by cos of the angle between the plane of polarization and the plane of oscillations of the electric component of the electromagnetic field.

Brightness of the visible light is related to the amount of energy the light carries.
Analysis shows that the amount of energy carried by a single ray of light is proportional to a square of its amplitude. We will address the logic behind this in the next lecture dedicated to energy of light.
Knowing this, we can say that the amount of energy of a single ray of light after going through the polaroid is less than the original amount by a factor cos²(θ).
So, the brightness of a single ray of light will diminish after polarization by cos²(θ). This is Malus Law.

This rule corresponds to the observable phenomena of light.
Consider a single ray of light with oscillations coinciding with a polarization plane. It means, θ=0 and cos(θ)=1, that is the ray goes through without any weakening.
On the other hand, if the plane of oscillations of the electromagnetic field is perpendicular to a polarization plane, θ=90° and cos(θ)=0, that is there is no light behind the polaroid.